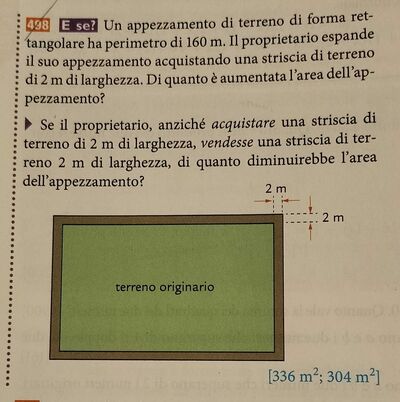
Un appezzamento di terreno di forma rettangolare ha perimetro di 160 m. Il proprietario espande il suo appezzamento acquistando una striscia di terreno di 2 m di larghezza. Di quanto è aumentata l'area dell'appezzamento?
Se il proprietario, anziché acquistare una striscia di terreno di 2 m di larghezza, vendesse una striscia di terreno 2 m di larghezza, di quanto diminuirebbe l'area dell'appezzamento?
194
punti
Livello 1
Siano x ed y le dimensioni iniziali per cui si ha:
xy= area terreno rettangolare; 2(x+y)=perimetro=160 m
La superficie nuova vale:
(x + 4)·(y + 4) = x·y + 4·x + 4·y + 16
se si sottrae la superficie di partenza:
x·y + 4·x + 4·y + 16 - x·y = 4·x + 4·y + 16=2*perimetro+16=
=2·160 + 16 = 336 m^2
Se invece vendesse una striscia di 2 metri di larghezza attorno al perimetro:
(x - 4)·(y - 4) - x·y = - 4·x - 4·y + 16=-2*perimetro+16=- 2·160 + 16 = -304 m^2
cioè perderebbe 304 m^2 del suo terreno
94739
punti
Genius II
@lucianop nella risoluzione dell' espressione 4·x + 4·y + 16 perche' ti torna 2*160+16? come si eliminano il 4x+4y?
perché: 4·x + 4·y è 2 volte il perimetro (il perimetro è un dato del problema: 160 m)
nuova area in aumento
(a+4)*(b+4) = ab+4b+4a +16
vecchia area
ab
differenza aree = (ab+4b+4a +16) -ab = 4a+4b+16
4a +4b = 2(2a+2b) = doppio perimetro
differenza aree = 2*160+16 = 336 m^2
nuova area in diminuzione
(a-4)*(b-4) = ab-4b-4a +16
vecchia area
ab
differenza aree = (ab-4b-4a +16) -ab = -4a-4b+16
4a +4b = 2(2a+2b) = doppio perimetro
differenza aree = -2*160+16 = -304 m^2
114341
punti
Genius II
