esercizio

Triangolo isoscele:

base $b= 6 : \frac{5}{6}=6×\frac{6}{5}=7,2~cm$;

perimetro $2p= b+2lo = 7,2+2×6 = 19,2~cm$.

a) Rombo:

diagonale minore $d= 19,2~cm$;

diagonale maggiore $D= 44,8-19,2 = 25,6~cm$.

b) Rettangolo:

perimetro $2p= 19,2~cm$;

semiperimetro o somma delle due dimensioni $p= \frac{19,2}{2}=9,6~cm$;

dimensione minore $=\frac{9,6}{7+17}×7 = \frac{9,6}{24}×7 = 2,8~cm$;

dimensione maggiore $=\frac{9,6}{7+17}×17 = \frac{9,6}{24}×17 = 6,8~cm$.

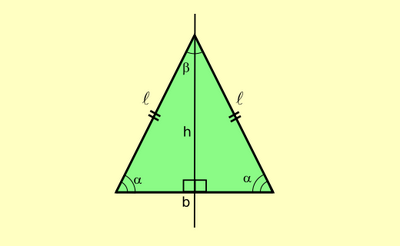
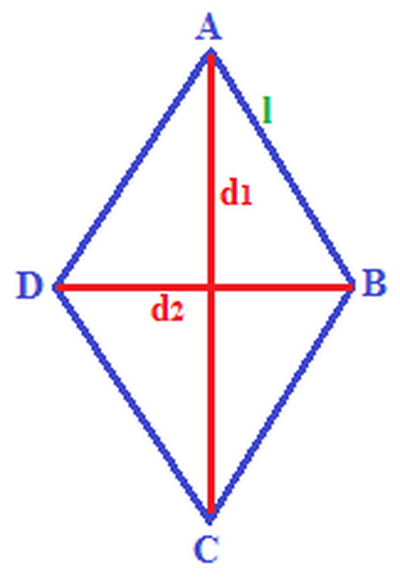
La somma della diagonali di un rombo misura 44,8 cm e la minore ha la stessa lunghezza del perimetro 2p di un triangolo isoscele. Il lato obliquo ℓ del triangolo misura 6 cm ed è 5/6 della base b 

triangolo isoscele 

Calcola  la misura del perimetro 2p

ℓ = 6 = 5b/6

base b = 36/5 = 72/10 = 7,2 cm 

perimetro 2p = 2ℓ+b = 12+7,2 = 19,2 cm 

rombo

Calcola  la misura di ciascuna diagonale; 

d2 = 2p = 19,2 cm

d1 = 44,8-19,2 = 25,6 cm 

rettangolo 

Calcola la misura delle dimensioni di un rettangolo isoperimetrico al triangolo che ha la  dimensione at pari a 7/17 di bs 

 2p = 19,2 cm

p = 19,2/2 = bs+7bs/17 

9,6 = 24bs/17

bs = 9,6*17/24 = 6,80 cm 

at = 6,80*7/17 = 2,80 cm