[Risolto] esercizio

@numus

CPQ è un triangolo isoscele sulla base PQ in quanto CP e CQ sono raggi. 

Quindi:

PH=HQ= 4 cm (in quanto l'altezza relativa alla base di un triangolo isoscele è anche mediana) 

Per il teorema della secante e della tangente, possiamo dire che:

SPST 

Con:

SK=PH=4 cm

SP=8 cm

Si ricava:

ST= 2 cm

TP= SP - ST = 8 - 2 = 6 cm

Il triangolo CPT è isoscele sulla base PT

CH=TP/2 = 3 cm

Possiamo quindi calcolare il raggio della circonferenza di centro C. 

R= 5 cm (terna pitagorica 3-4-5)

(CH = 3, PH =4)

Scelto come origine del sistema di riferimento il punto C(0,0) la circonferenza ha quindi equazione:

x² + y² = 25

Con la scelta fatta i due punti T, Q appartenenti alla circonferenza hanno coordinate:

T=( - 3, 4)

Q=( 3,4)

Utilizziamo le formule di sdoppiamento per scrivere le equazioni delle due rette tangenti alla conica nei punti richiesti. 

t: - 3x+4y = 25

q: 3x - 4y = 25

"e raggio e" vorrebbe dire che il raggio si chiama "e"? FOLLIA, dove c'è un circolo solo il raggio si chiama "r", da che mondo è mondo!
------------------------------
A) "fissato un opportuno sistema di riferimento" con unità di lunghezza U = 4 cm.
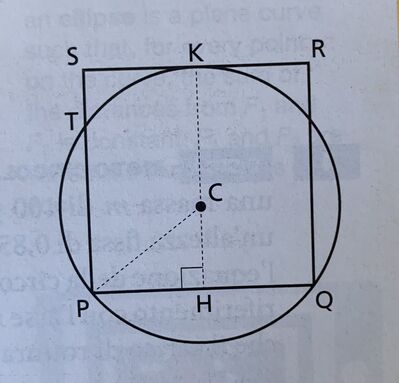
* H(0, 0), P(- 1, 0), Q(1, 0), R(1, 2), S(- 1, 2), C(0, h), K(0, 2), T(- 1, k)
------------------------------
B) "determina l'equazione della circonferenza"
C(0, h) è l'unico punto del piano equidistante da PQK, del cui triangolo è circumcentro, e la comune distanza è il raggio "r".
* |CP|^2 = |CQ|^2 = |CK|^2 = r^2 = q ≡
≡ h^2 + 1 = h^2 + 1 = (h - 2)^2 = r^2 = q ≡
≡ h^2 + 1 = (h - 2)^2 = q = r^2 ≡
≡ (h = 3/4) & (q = 25/16) & (r = 5/4)
da cui
* C(0, 3/4)
la circonferenza
* Γ ≡ x^2 + (y - 3/4)^2 = 25/16 ≡
≡ 2*x^2 + 2*y^2 - 3*y - 2 = 0
e l'intersezione
* (x = - 1) & (x^2 + (y - 3/4)^2 = 25/16) ≡ T(- 1, 3/2)
------------------------------
C) "Trova la tangente in T e verifica che è parallela a quella in Q"
Consegna un po' contorta.
---------------
C1) Il segmento QT è lungo 5/2, giace sulla retta y = - (3/4)*(x - 1), ha punto medio C(0, 3/4); quindi è un diametro e le tangenti nei suoi estremi sono parallele.
---------------
C2) Le tangenti negli estremi del diametro QT gli sono ortogonali; quindi sono elementi del fascio
* t(k) ≡ y = (4/3)*x + k
e si determinano dai vincoli d'appartenenza
* in Q(1, 0): 0 = (4/3)*1 + k ≡ k = - 4/3 → t(- 4/3) ≡ y = (4/3)*(x - 1)
* in T(- 1, 3/2): 3/2 = (4/3)*(- 1) + k ≡ k = 17/6 → t(17/6) ≡ y = (8*x + 17)/6