ESERCIZIO 1
Traccia i grafici delle parabole venti le seguenti equazioni, dopo aver detrminato di ciascuna il vertice V, l'asse e altri 4 suoi punti:
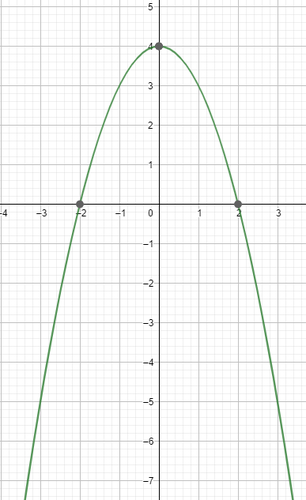
y=-x^2+4
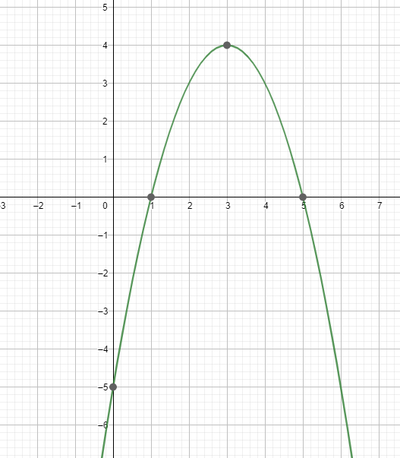
y=-x^2+6x-5
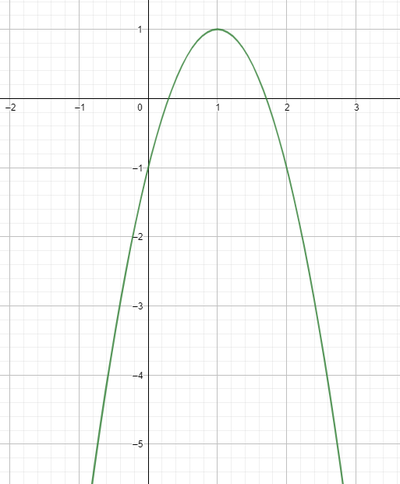
y=-2x^2+4x-1
ESERIZIO 2
Traccia il grafico delle parabole aventi le seguenti equazioni, dopo averne individuato il vertice e i punti d'intersezione con gli assi cartesiani
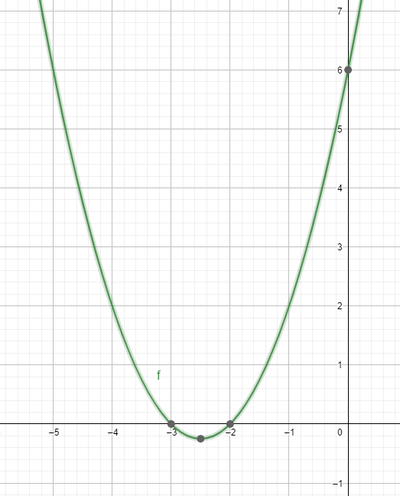
$y=x^2+5x+6$
ESERIZIO 3
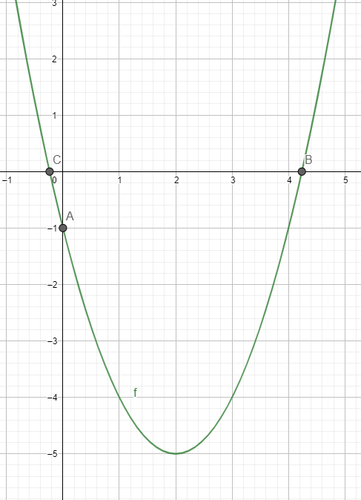
Traccia il grafico della parabola di equazione $y=x^2-4x-1$ e determina l'area del triangolo formato dai suoi punti d'intersezione con gli assi cartesiani