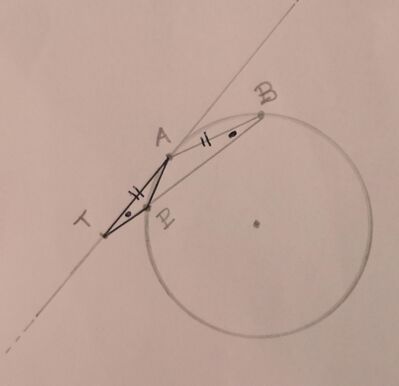
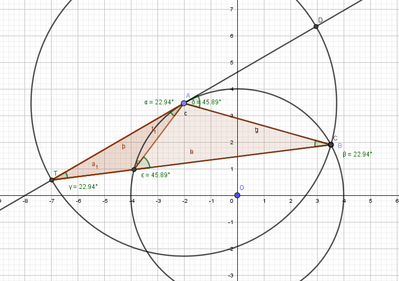
Data una circonferenza di centro O, sia AB una sua corda. Traccia la tangente in A alla circonferenza. Considera su tale tangente il punto T, appartenente al semipiano avente come origine la retta AB che contiene O, tale che AT ~= AB. Indica con P il punto d'intersezione della retta BT con la circonferenza e dimostra che il triangolo APT è isoscele sulla base AT.
3
punti
Livello 0
Il triangolo ABT è isoscele per costruzione sulla base BT essendo AT = AB
Dal teorema della secante e della tangente ad una circonferenza sappiamo che:
TB : TA = TA : TP
I triangoli APT e ABT sono quindi simili poiché hanno due lati in proporzione e l'angolo compreso congruente.
In particolare l'angolo ABT (= ATB poiché il triangolo ATB è isoscele) è congruente all'angolo TAP.
Per la proprietà transitiva sono quindi congruenti gli angoli TAP e ATP.
Il triangolo APT è isoscele sulla base AT
76754
punti
Genius II
Ciao
Provo a scriverti come ho dimostrato la tesi.
Intanto sappiamo che il triangolo ABT è isoscele per costruzione, quindi avrà gli angoli alla base uguali, più precisamente:
ATB = ABT
Poi faccio la seguente considerazione
I triangoli ABT e APT sono simili poiché:
Ne segue l’uguaglianza fra i seguenti angoli:
ATB = ABT = TAP
quindi
ATB = TAP
Quindi il triangolo ATP, avendo gli angoli alla base uguali, è isoscele.
9955
punti
Livello 7
Con riferimento alla figura allegata sopra, penso che tu ci possa arrivare....
Adesso vado a nanna!
94774
punti
Genius II
