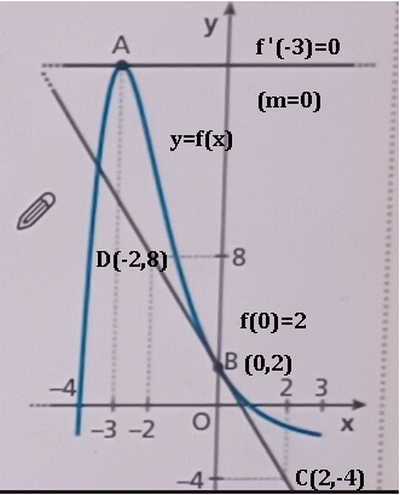
La curva $\mathscr{C}$ a fianco rappresenta il grafico di una funzione $f(x)$ definita e derivabile nell'intervallo $[-4 ; 3]$. Il punto $A$ di ascissa -3 e il punto $B(0 ; 2)$ appartengono alla curva $\mathscr{C}$. Nel grafico sono rappresentate anche le tangenti a $\mathscr{C}$ nei punti $A$ e $B$, con la tangente in $A$ orizzontale.
a. Osservando il grafico, determina $f^{\prime}(-3), f(0)$ e $f^{\prime}(0)$.
b. La funzione $f(x)$ è definita in $[-4 ; 3]$ da $f(x)=a+(x+b) e^{-x}$, dove $a$ e $b$ sono parametri reali. Dopo aver calcolato $f^{\prime}(x)$, determina i valori di $a$ e $b$.
(Francia, Francia continentale, Baccalauréat, Serie L, 2015, esercizio 3, parte A)
[a) $f^{\prime}(-3)=0, f(0)=2, f^{\prime}(0)=-3$; b) $\left.a=-2, b=4\right]$