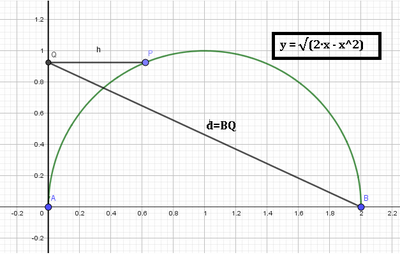
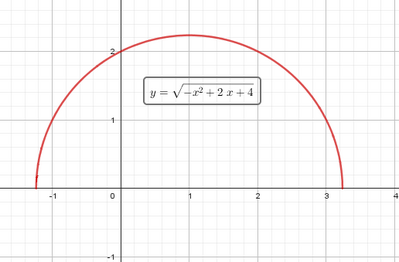
Su una semicirconferenza di diametro $A B$ e raggio 1, considera un punto $P$ e indica con $Q$ la sua proiezione sulla tangente alla semicirconferenza passante per $A$. Indica con $x$ la distanza di $P$ da $Q$ e con $y$ la misura del segmento $B Q$. Esprimi $y$ in funzione di $x$ e traccia il grafico della funzione ottenuta, mettendo in evidenza il tratto relativo al problema. $\left[y=\sqrt{4+2 x-x^2}\right.$, con $\left.0 \leq x \leq 2\right]$
potreste svolgerlo. A me esce y= radice di 5-x^2
92
punti
Livello 1
Ciao. Ho scelto il sistema di riferimento di figura:
Quindi ho considerato la funzione: y = √(2·x - x^2)
che esprime la semicirconferenza del testo. Così facendo P ha coordinate: [x, √(2·x - x^2)]
da cui : 0 ≤ x ≤ 2
Quindi:
[0, √(2·x - x^2)] sono le coordinate di Q
[2, 0] sono le coordinate di B
Quindi questa opportuna scelta mi permette di dire che:
d=BQ = √((2 - 0)^2 + √(2·x - x^2)^2)
d = √(- x^2 + 2·x + 4) con 0 ≤ x ≤ 2
Nel sistema di riferimento (x,y) esprime una semicirconferenza:
N.B. (y = √(- x^2 + 2·x + 4))^2
y^2 = - x^2 + 2·x + 4----> x^2 + y^2 - 2·x - 4 = 0
rappresenta la circonferenza completa con centro in C(1,0) e raggio r=√(1^2 + 0^2 + 4) = √5
quindi di equazione: (x-1)^2+y^2=5
94640
punti
Genius II
