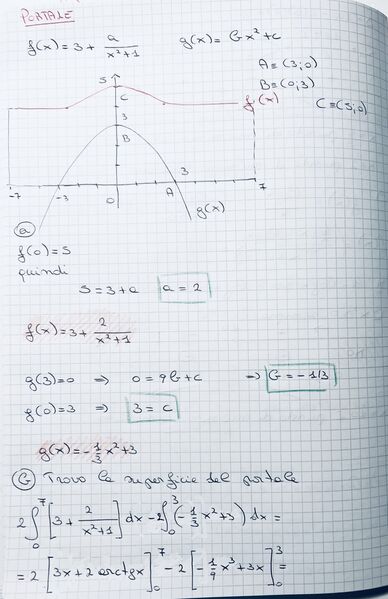
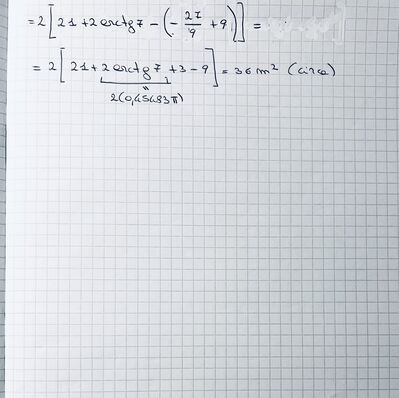Il portale All'ingresso di un parco pubblico c'è un portale che ha il profilo mostrato in figura. Il portale deve essere rivestito di marmo, che viene venduto in lastre quadrate di $1 \mathrm{~m}^2$ ciascuna.
a. Le equazioni delle curve che delimitano il portale sono $f(x)=3+\frac{a}{x^2+1}$ e $g(x)=b x^2+c$. Trova $a, b$ e $c$.
b. Determina il numero minimo di lastre necessarie per rivestire tutta la facciata.
Buonasera, ho un problema solo con il secondo punto perché il primo mi è venuto senza problemi. Comunque per risolvere il punto b ho pensato, dato che ho la figura, di calcolarmi la superficie del portale facendo l’integrale di f(x) - integrale di g(x), nell’intervallo [0;7] per f(x) e [0;3] per g(x). Ciò che salta fuori è un valore approssimato a 38 (ho poi moltiplicato il risultato dell’area nell’intervallo indicato •2) e non capisco come trovare 36.
Spero di essermi spiegata.
Grazie e buona serata.