[Risolto] equazione arco di circonferenza

consideriamo una circonferenza generica di equazione x^2+y^2+ax+by+c=0 di centro C(-a/2;-b/2).

se la circonferenza passa per l'origine sappiamo per certo che c=0.

siccome il punto P(-1;1) appartiene alla circonferenza sappiamo anche che possiamo sostituire le sue coordinate all'interno dell'equazione della circonferenza: 1+1-a+b=0 , cioè a=b+2

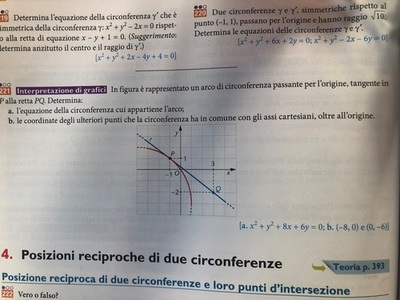
ora calcoliamo il coefficiente angolare della retta PQ:

mPQ= (yP-yQ)/(xP-xQ)= -3/4

noi sappiamo che quando una retta è tangente ad una circonferenza, sicuramente il raggio della circonferenza è perpendicolare a questa retta. Troviamo quindi il coefficiente angolare della perpendicolare a PQ:

m= -1/mPQ = 4/3

ora troviamo la retta su cui poggia il raggio, nonchè la retta passante per il centro: si tratta di una retta con m=4/3 passante per P(-1;1)

r: 4x-3y+7=0

siccome il centro C appartiene a questa retta, possiamo sostituire le sue coordinate che sono x=-a/2 e y=-b/:

-2a + 3b/2 + 7 = 0  ---> 4a - 3b -14 = 0  (moltiplico per -2)

da prima ci ricordiamo però che a=b+2, quindi facciamo l'ultima sostituzione:

4(b+2) - 3b -14=0 -----> b=6 ; a=8

la circonferenza ha equazione: x^2 + y^2 +8x +6y=0

 

SECONDO PUNTO

per il secondo punto basta studiare due casi:

1) x=0

se annulliamo la x si ottiene y^2 + 6y=0  che ha come soluzioni y=0 e y=-6, quindi i punti sono A(0;0) e B(0;-6)

2)y=0

se annulliamo la y si ottiene x^2 +8x=0 con soluzioni x=0 e x=-8. I punti sono A(0;0) e C(-8;0)