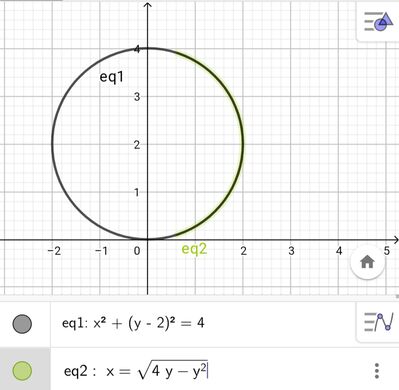
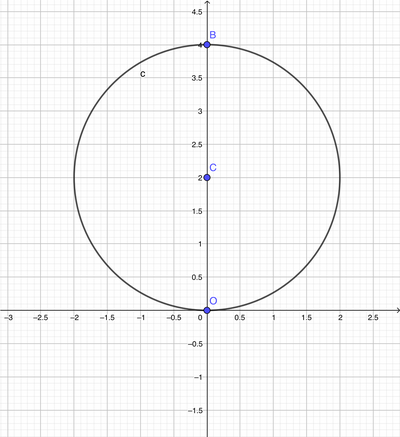
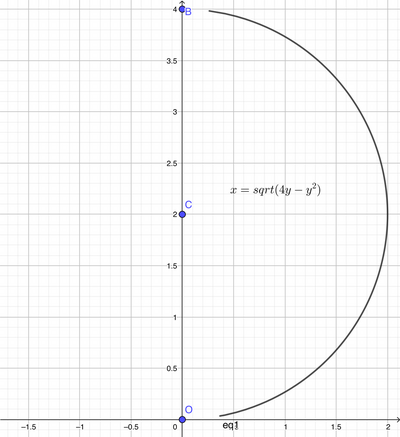
Scrivi l'equazione della semicirconferenza che ha diametro OB, con O origine degli assi , B (0;4), e che si trova nel I' quadrante
Risposta : x = rad 4y-y^2.
Ho calcolato il raggio e applicato la formula y = rad r^2 - x^2, ma il risultato non mi torna. Qualcuno mi può, gentilmente dare un aiuto? Grazie a tutti come sempre.
1502
punti
Livello 1
Il centro C della circonferenza avente diametro OB ha coordinate:
C=[(xO + xB) /2 ; (yO + yB) /2] = (0,2)
Il raggio è:
R= OB/2 = 2
L'equazione della circonferenza di centro C , raggio R=2 è :
x² + (y - 2)² = 2²
Possiamo quindi determinare l'equazione della semicirconferenza mettendo a sistema l'equazione della circonferenza con la condizione x>0
{x² + (y - 2)² = 2²
{x>0
Sviluppando i calcoli si ottiene:
{x² = 4y - y²
{x > 0
Da cui si ricava:
x= radice (4y - y²)
76753
punti
Genius II
Considera la circonferenza di centro C(0,2) e raggio pari a r =2.
quindi: x^2+(y-2)^2=4
Risolvi rispetto a x e considera la soluzione con x>0
x^2+y^2-4y+4=4
y^2-4y+x^2=0
x^2= 4y-y^2
ottieni
x=sqrt(4y-y^2)
scartando quella negativa.
94670
punti
Genius II
Il diametro é OB per cui il centro C si trova in (0;2)
e il raggio é r = |4 - 0|/2 = 2
La circonferenza ha equazione
(x - 0)^2 + (y - 2)^2 = 2^2
x^2 + y^2 - 4y + 4 - 4 = 0
x^2 + y^2 - 4y = 0
x^2 = 4y - y^2
e il fatto che siamo nel I quadrante ci fa scegliere il segno positivo per x :
x = rad(4y - y^2).
47871
punti
Livello 7
La circonferenza Γ di cui si chiede la metà destra ha centro C(0, 2), raggio r = 2 ed equazione
* Γ ≡ x^2 + (y - 2)^2 = 2^2 ≡
≡ x^2 = 2^2 - (y - 2)^2 = 4 - (y^2 - 4*y + 4) ≡
≡ x^2 = 4*y - y^2 ≡
≡ x = ± √(4*y - y^2)
da cui si prende la sola metà destra con
* x = √(4*y - y^2)
57383
punti
Genius I
