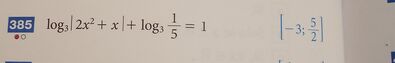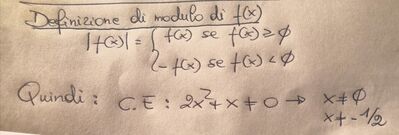In completo disaccordo con buona parte degli altri responsori di questo sito sostengo che la condizione di esistenza del logaritmo naturale di variabile reale [ln(u)] NON E AFFATTO "u > 0", ma solo "u != 0".
Mi conforta in tale convinzione il parere di Eulero che, condividendola, scoprì (~ 1748) quella che chiamò "formula del Diavolo": e^(i*π) = - 1.
E' solo quando occorre che la funzione logaritmo abbia valori reali (p.es. nelle disequazioni con diseguaglianza d'ordine) che si deve usare la condizione "u > 0": ma un'equazione può benissimo essere soddisfatta da valori negativi della variabile.
------------------------------
L'esercizio
385) log(3, |2*x^2 + x|) + log(3, 1/5) = 1
è un'equazione, quindi occorre e basta escludere i valori x ∈ {- 1/2, 0} che annullano il primo argomento il quale, essendo un valore assoluto, negativo non può essere; perciò la procedura risolutiva è come segue.
* (log(3, |2*x^2 + x|) + log(3, 1/5) = 1) & (x != - 1/2) & (x != 0) ≡
≡ (ln(|2*x^2 + x|/5) = ln(3)) & (x != - 1/2) & (x != 0) ≡
≡ (e^ln(|2*x^2 + x|/5) = e^ln(3)) & (x != - 1/2) & (x != 0) ≡
≡ (|2*x^2 + x|/5 = 3) & (x != - 1/2) & (x != 0) ≡
≡ (|2*x^2 + x| = 15) & (x != - 1/2) & (x != 0) ≡
≡ ((2*x^2 + x = - 15) oppure (2*x^2 + x = 15)) & (x != - 1/2) & (x != 0) ≡
≡ ((radici complesse) oppure (x = - 3) oppure (x = 5/2)) & (x != - 1/2) & (x != 0) ≡
≡ (x = - 3) oppure (x = 5/2)
che è proprio il risultato atteso.
------------------------------
RISPOSTE AI QUESITI
---------------
1) "C.E 2x^2+x>0 ... Giusto ?" NO
Il valore assoluto non può essere negativo, basta escludere che sia zero.
---------------
2a) "essendo ... posso fare lo stesso ragionamento delle C.E ?" NO
Quello era un ragionamento errato.
---------------
2b) "o devo ... -2x^2-x ?" NO
Non si tratta di un dilemma a due corni, è un polilemma: oltre alle due due possibilità ci sono anche quelle delle procedure corrette. Sopra te ne ho mostrato una.