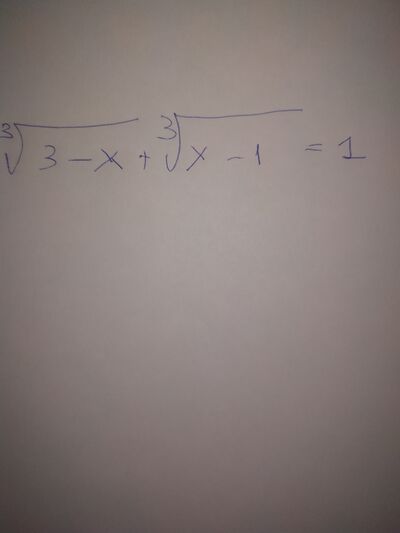[Risolto] Equazione irrazionale

La flessibilità della sintassi italiana consente di esprimere sfumature semantiche assai raffinate, ma non tutti sono capaci di farne uso. Nella maggior parte delle domande qui pubblicate l'uso di un verbo al condizionale serve solo a esprimere cafonaggine sia in forma di bigotta piaggeria ("potreste aiutarmi?" e come no, il sito è fatto apposta!) che in forma di arroganza infantile ("qualcuno riuscirebbe ...?" ma che fai, sfidi?).
Ricambierò il piacere che mi fa leggere un uso corretto ed elegante ("... mentre i risultati dovrebbero essere ...") clickando un cuoricino a fianco alla domanda, e vengo al merito.
------------------------------
* (3 - x)^(1/3) + (x - 1)^(1/3) = 1 ≡
≡ f(x) = (3 - x)^(1/3) + (x - 1)^(1/3) - 1 = 0
da cui
* f(2) = 1 != 0
* f(3) = 2^(1/3) - 1 != 0
e ciò merita il click al tuo "dovrebbero".
------------------------------
Circa "Ma viene un risultato contorto" serve un po' di pazienza in più.
* (3 - x)^(1/3) + (x - 1)^(1/3) = 1 ≡
≡ (3 - x)^(1/3) = 1 - (x - 1)^(1/3) ≡
≡ ((3 - x)^(1/3))^3 = (1 - (x - 1)^(1/3))^3 ≡
≡ 3 - x = - x + 3*(x - 1)^(2/3) - 3*(x - 1)^(1/3) + 2 ≡
≡ 3*(x - 1)^(2/3) - 3*(x - 1)^(1/3) - 1 = 0 ≡
≡ 3*u^2 - 3*u - 1 = 0 ≡
≡ (u = (1 - √(7/3))/2) oppure (u = (1 + √(7/3))/2) ≡
≡ ((x - 1)^(1/3) = (1 - √(7/3))/2) oppure ((x - 1)^(1/3) = (1 + √(7/3))/2) ≡
≡ (x = 2 - 2*√(7/3)/3) oppure (x = 2 + 2*√(7/3)/3)
Tutto sommato il risultato è irrazionale, ma niente di che; contorto m'è sembrato il giro dalle vigne dell'arciprete che serve per arrivarci.
Se un caso del genere sorge da un problema pratico, dal momento che la soluzione simbolica non mostra particolari perspicuità (così come l'approssimazione 2*√(7/3)/3 ~= 1.01835), tanto vale usare fin da subito metodi grafico-numerici.

Sicuramente 2 e 3 non sono soluzioni, almeno non con questa traccia. 

Poi, il procedimento é corretto.