Non so dire quanto dipenda dalle Direttive Ministeriali sui libri scolastici (che non ho letto) e quanto dalla neghittosità di Autori, Editori e Consigli di Classe, ma TROVO ORRIBILE L'INGANNO AI DANNI DEGLI ALUNNI che consiste nel dar loro libri che nominano "un'ellisse" o "un'iperbole" dando per scontato che, in assenza di specificazioni, si debba intendere "centrata nell'origine e con assi gli assi x e y".
Un libro serio, da Università, fa il contrario: in assenza di specificazioni SI DEVE INTENDERE forma generale con sei parametri.
------------------------------
Circa il tuo allarme sul fatto che "... ti sparisce l'incognita m ..." (la pendenza, immagino) questo dipende dal metodo di calcolo della retta tangente: usando il calcolo delle rette polari si trovano anche le tangenti verticali senza bisogno di riconoscerle per ispezione come ha fatto @StefanoPescetto: un principiante svolge esercizi proprio allo scopo di sviluppare quelle competenze che ancora non possiede, come quella di "riconoscere per ispezione" le configurazioni significative.
------------------------------
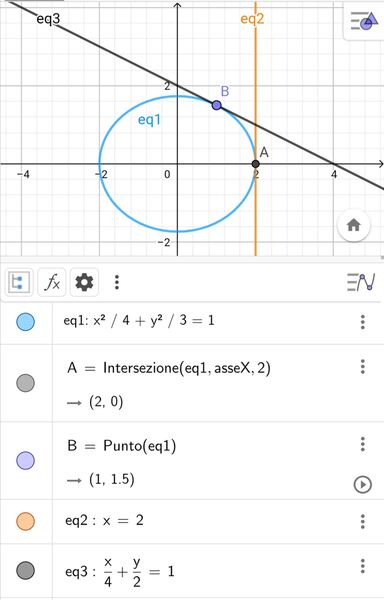
Qui ti mostro il calcolo della retta polare del polo A(2, 0) nella polarità indotta nel piano Oxy dalla presenza della conica
* Γ ≡ x^2/4 + y^2/3 = 1
poi, in fondo, ti scrivo un minipromemoria sull'argomento.
---------------
A) Ridurre l'equazione alla forma normale canonica f(x, y) = 0.
* Γ ≡ x^2/4 + y^2/3 = 1 ≡ 3*x^2 + 4*y^2 - 12 = 0
---------------
B) Sostituire: x^2 → 2*x; y^2 → 0*y; ottenendo
* 3*2*x + 4*0*y - 12 = 0
---------------
C) Semplificare per avere la retta tangente Γ in A:
* x = 2
che, ovviamente, è quella che dev'essere; ma la si è ottenuta calcolando e non riconoscendo.
==============================
PROBLEMA DELLE TANGENTI, RETTA POLARE, SDOPPIAMENTI
La retta polare p(Γ, P) del punto P(u, v), il polo, rispetto alla conica Γ si ottiene dall'equazione di Γ in forma normale canonica, "f(x, y) = 0", lasciandone inalterati i coefficienti e operandovi le sostituzioni (formule di sdoppiamento) seguenti:
* x^2 → u*x
* y^2 → v*y
* x*y → (v*x + u*y)/2
* x → (u + x)/2
* y → (v + y)/2
Secondo la posizione del polo rispetto alla conica si danno tre casi.
Se P è interno a Γ allora p(Γ, P) non interessa il problema delle tangenti.
Se P è su Γ allora p(Γ, P) è la tangente in P.
Se P è esterno a Γ allora p(Γ, P) interseca Γ nei punti di tangenza delle tangenti condotte da P.