Soluzione particolare mi è uscita (68,40)
Equazione omogena k(515,-303) k appartenente a z (qui ho più dubbi)
la soluzione generale 606x-1030y = (68,40) + k(515,-303)
Soluzione per k = 0 --> (68,40), k = 1 --> (583,-263), k =2 --> (1098,-566)
Sono giuste tutte queste soluzioni?
103
punti
Livello 1
@daniele11000 ...chiedi ad EidosM
Purtroppo non ho grande esperienza in questo settore.
Puoi confrontare con quanto indicato qui
https://www.andreaminini.org/matematica/identita-di-bezout
e sicuramente guadagni tempo se lo guardi tu che hai fresco l'argomento che se dovessi
(ri) studiarlo io.
Tuttavia ho buoni indizi che potrebbe essere giusto. Infatti la soluzione particolare (anche se
non so come l'hai trovata) soddisfa effettivamente l'equazione.
47870
punti
Livello 7
@eidosm Sisi utilizza lo stesso metodo del mio prof, la soluzione particolare la si ottiene effettuando l'algoritmo di euclide dell' MCD + coefficienti di Bezout, poni a(primo numero) e b(secondo numero con) i seguenti coefficienti unitari (1,0), (0,1) successivamente ad ogni divisione applichi la seguente formula (1,0) - quoziente ottenuto*(0,1) e alla fine ti ritrovi i coefficienti di bezout potendo scrivere l'mcd nella seguente forma: d= ax + by = MCD tra a e b
poi moltiplichi i coefficienti di Bezouè t in questo caso *4 nel primo caso e *-4 nel secondo caso e ti ricavi la soluzione particolare, perchè se non sbaglio l'MCD è 2.
Ho pensato anch'io che l'algoritmo fosse quello indicato ma non l'ho portato a termine perché mi avrebbe richiesto troppo tempo.
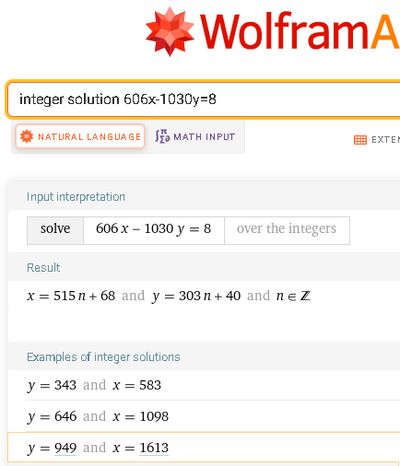
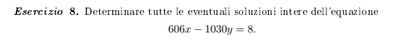* 606*x - 1030*y = 8 ≡
≡ 303*x - 515*y = 4 ≡
≡ y = (303*x - 4)/515
Per
* (x = 515*k + 68) & (k in Z)
si ha
* y = (303*(515*k + 68) - 4)/515 = 303*k + 40
------------------------------
"Sono giuste tutte queste soluzioni?"
---------------
1) "mi è uscita (68,40)" OK, per k = 0.
---------------
2) "k(515,-303) & (k in Z)" non capisco: significa (x, y) = (515*k, - 303*k)?
Se è così basta una verifica
* 606*515*k - 1030*(- 303*k) = 8 ≡
≡ 624180*k = 8 ≡
≡ k = 2/156045 che non mi sembra rientrare "in Z".
---------------
3) "606x-1030y = (68,40) + k(515,-303)" come sopra, la intendo come
* (x, y) = (68, 40) + k*(515, - 303) = (68 + 515*k, 40 - 303*k)
da cui
* 606*(68 + 515*k) - 1030*(40 - 303*k) = 8 ≡
≡ 4*(156045*k + 2) = 8 ≡
≡ 156045*k = 0
e questa, più che un'identità, mi sembra un'equazione.
---------------
4) "k = 0 --> (68,40), k = 1 --> (583,-263), k =2 --> (1098,-566)"
Verificarle è superfluo: discendono dalla "3", che ci vuoi fare?
==============================
DETTAGLI
---------------
* EDO ≡ 606*x - 1030*y = 8 (Equazione Diofantea Originale)
* MCD(606, - 1030) = MCD(1030, 606) = 2
* 8 = 2*4 + 0 ≡ ED è risolubile e si riduce a
* ED ≡ 303*x - 515*y = 4
---------------
* EDU ≡ 303*x - 515*y = 1 (ED Unitaria)
* - 515 = (- 2)*303 + 91 ≡ 91 = 2*303 - 515
* 303 = (+ 3)*91 + 30 ≡ 30 = 303 - 3*91
* 91 = (+ 3)*30 + 1 ≡ 1 = 91 - 3*30 ≡
≡ 1 = 91 + 9*91 - 3*303 = 10*91 - 3*303 ≡
≡ 1 = 10*(2*303 - 515) - 3*303 = 10*2*303 - 10*515 - 3*303 = 10*2*303 - 3*303 - 10*515 ≡
≡ 1 = 17*303 - 10*515
da cui
* (X = 17) & (Y = 10)
---------------
Con k in Z
* (x = 4*17 - 515*k) & (y = 4*10 - 303*k) ≡
≡ (x = 68 - 515*k) & (y = 40 - 303*k) ≡
≡ (x = 515*k + 68) & (y = 303*k + 40)
57383
punti
Genius I
@exprof Ok grazie mille, anche se ho notato che la risolviamo in modi differenti, ho appena ricevuto conferema dal professore tramite ricevimento ed è corretta.
Io ho utilizzato algoritmo dell'MCD + coefficienti di Bezout
@Daniele11000
Beh, anch'io!
Mi pare strano che tu non l'abbia riconosciuto, l'ho etichettato "ED Unitaria".
@exprof Purtroppo mi perdo facilmente a volte con simbologia ed ecc 😆
(68,40) è giusta:
94663
punti
Genius II
