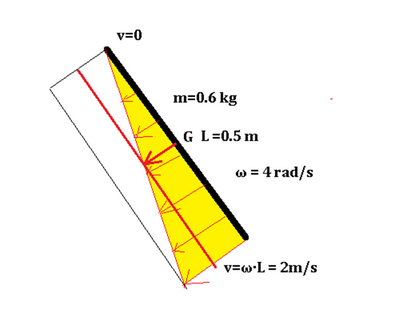
Un'asta omogenea di massa $m=0,60 kg$ e lunghezza $l=0,50 m$ ruota su un piano orizzontale attorno a una sua estremità con velocità angolare $\omega_{0}=4,0 rad / s$. A un dato istante il perno che tiene ferma l'estremità dell'asta si rompe e l'asta è libera di muoversi sul piano. Trascura tutti gli attriti.
Spiega perché l'asta trasla, ruotando attorno al suo centro.
Calcola l'energia cinetica finale dell'asta.
$[0,33]]$
Vedi figura
279
punti
Livello 1
In assenza di attriti, l’asta mantiene in ogni suo punto la velocità acquisita sino a quel momento. Siccome tali velocità hanno andamento triangolare ed indirizzate nello stesso verso e direzione l’asta traslerà mantenendo l’andamento triangolare delle velocità.
Questo implica una traslazione dell’asta ed una rotazione in corrispondenza del suo baricentro nel momento stesso che venga tolto il perno ove avveniva la rotazione.
E’ quindi pensabile che il moto dell’asta sia composto da una traslazione dell’asta nel suo baricentro G con valore pari a 1 m/s e da una rotazione dell’asta attorno al suo baricentro stesso.
Quindi l’energia cinetica è somma di due contributi:
Ec=1/2·m·v^2 + 1/2·I·ω^2 =1/2·0.6·1^2 + 1/2·(1/12·0.6·0.5^2)·4^2 = 0.4 J
94640
punti
Genius II
Ringrazio
