Un condensatore piano ha le armature di forma circolare e raggio R. Supponi di poter trascurare gli effetti al bordo.
Determina l'espressione del campo magnetico indotto B(t) a distanza r<R dall'asse del condensatore se l'intensità del campo elettrico tra le armature varia secondo la legge E(t)=E0 f(t), dove f(t) =8/(t^2+4)
Cosa cambia nell'espressione trovata se r>R?
39
punti
Livello 0
scusami non so usare questi siti, mi sono iscritta apposta. la disperazione fa male
ciao, ho lo stesso elaborato, sono disperata se riesci a risolverlo riusciresti a farmi sapere?
Si in teoria l'ho risolto
Scusa, come si fa?
https://www.sosmatematica.it/forum/domande/aiuto-19/#post-22094
legge di Ampere-Maxwell
circuitazione di B al contorno di S = mu0*eps0*flusso di dE/dt attraverso S
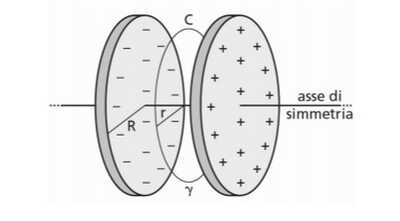
per la simmetria e l'uniformità si avrà:
B(r)*C(r) = mu0*eps0*S(r)*dE/dt ---> B(r)*2*pi*r = mu0*eps0*pi*r²dE/dt ---> B(r)*2 = mu0*eps0*r*d(Eo*f)/dt ---> B(r)= mu0*eps0*Eo*r/2*df/dt ---> B(r) = mu0*eps0*Eo*r/2*(-(16 t)/(t^2 + 4)^2 ) --->
B(r) = - mu0*eps0*Eo*r*(8 t)/(t^2 + 4)^2
Cosa cambia nell'espressione trovata se r>R?
il campo E NON ESISTE PIù E IL FLUSSO di dE/dt non cambia più con r ma si ferma a R...(***)
B(r)*C(r) = mu0*eps0*S(R)*dE/dt ---> B(r)*2*pi*r = mu0*eps0*pi*R²dE/dt ---> B(r)*2*r = mu0*eps0*R²dE/dt ---> B(r) = mu0(eps0/ (2*r)) *R²dE/dt ---> B(r) = mu0(eps0/ (2*r)) *R²*Eo*df/dt ---> B(r) = mu0(eps0/ (2*r)) *R²*Eo* (-(16 t)/(t^2 + 4)^2 )
----------------
(***) si osserva che (eps0/ (2*r)) *R²dE/dt = (1/ (2*r)) *R²dD/dt = (1/ (2*r)) *R²dsigma/dt = (1/ (2*r)) *R² (1/(pi*R²))dq/dt = (1/ (2*r)) *R² (1/(pi*R²)) i(t) = (1/ (2*r)) (1/(pi)) i(t)
dove i(t) = dq/dt è "anche " la corrente istantanea che affluisce al condensatore.
5664
punti
Livello 5
Grazie mille per avermi risposto, mi è sorta una curiosità: cosa accadrebbe nel caso il cui i raggi coincidessero(r=R)?
nice job
