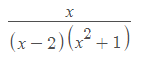[Risolto] Dubbio sulle condizioni di esistenza di una frazione algebrica

Le condizioni di esistenza di una frazione algebrica riguarda esclusivamente il denominatore che deve essere posto diverso da zero per ammettere l'esistenza di tale frazione.

D: $(x-2)(x^2+1)\neq 0$

$(x-2) \neq 0 \Rightarrow x\neq 2$

$(x^2+1)\neq 0 \Rightarrow x^2 \neq  -1$ 

Dalla seconda, qualsiasi numero al quadrato è sempre diverso da -1, quindi è sempre verificata.

Quindi la funzione è verificata per: $\forall x$ - {2}

Se x=2, sostituiamo 2 nella funzione $ \frac{2}{(2-2)(2^2+1)}=\frac{2}{0}$

quindi la funzione non è definita, infatti tale valore è escluso dalle C.E

Il numeratore non bisogna essere studiato per stabilire le condizioni di esistenza, ma doveva essere studiato se il testo richiedeva lo studio di tale funzione.

La frase "Una frazione algebrica è diversa da zero se e solo se il suo denominatore e numeratore sono non nulli" è un'affermazione vera anche se puo' trarre in inganno. 

innanzitutto vedere se una frazione è = zero non significa che non esiste. 

Per conoscere l'esistenza devi solo guardare il denominatore e trovare i valori per i quali si annulla. La frazione NON ESISTE per i valori per i quali si annulla il denominatore.

Se sei interessata a sapere per quali valore una frazione è zero devi cercare i valori che annullano il numeratore (sempre facendo attenzione che tali valori  facciano parte del campo di esistenza che avrai analizzato precedentemente altrimenti la frazione non esiste )

Nella frase riportata l'interesse è affermare quando la frazione non è zero. Lo è giustamente quando il numeratore non è zero e contemporaneamente esiste il denominatore (cioè il denominatore è diverso da zero altrimenti non abbiamo proprio l'esistenza della frazione)

In riferimento alla domanda "Una frazione algebrica è diversa da zero se e solo se il suo denominatore e numeratore sono non nulli" è deduttivamente scorretta. Vediamo di capire il perché. Facendo abuso di un linguaggio formalizzato cerchiamo di tradurre la precedente proposizione in simboli per poi dedurre, partendo da eventuali premesse, una data conclusione. Poniamo 

$A$ $:$ $=$ $Frazione$ $algebrica$

$B$ $:$ $=$ $Numeratore$

$C$ $:$ $=$ $Denominatore$

In linguaggio simbolico otteniamo :

$A$  $\neq$  $0$  $\iff$  $\bigl($ $B$  $\neq$  $0$ $\bigr)$  $\land$  $\bigl($ $C$  $\neq$  $0$ $\bigr)$.

$Equivalentemente$ :

$A$  $=$  $0$  $\iff$  $\bigl($ $B$  $=$  $0$ $\bigr)$  $\lor$  $\bigl($ $C$  $=$  $0$ $\bigr)$  $\space$ $\bigl($ $Teorema$ $di$ $De$ $Morgan$ $\bigr)$

Come possiamo notare, se supponiamo vero questo enunciato otterremo sicuramente una contraddizione. Nel caso in cui supponiamo che il denominatore sia uguale a $0$ e numeratore diverso da $0$ otterremo una frazione di questo tipo $\displaystyle\frac{ a }{ 0 }$ con $a$ $\neq$ $0$ $\in$ $R$. Ma questa frazione senza ombra di dubbio non può esistere in $R$ poichè la divisione per $0$ non è consentita. Quindi avendo una frazione di questo tipo non possiamo certamente dedurre che la frazione sia uguale a $0$ ( almeno non nella nostra realtà ) non dovrebbe neanche avere senso attribuire un valore di verità quando ci troviamo di fronte a situazioni del genere. Dunque a mio parare, la proposizione risulta essere deduttivamente scorretta ( o come dicono i logici "$fallacia$ $dell$'$argomentazione$" ). Ma in logica, come ben sappiamo vige il principio del terzo escluso in cui una proposizione risulta sempre essere vera o falsa senza una via di mezzo. Per contro cerchiamo di rettificare la proposizione di partenza modificando alcuni parametri. Dunque :
supponendo il denominatore diverso da $0$ la frazione risulta essere uguale a $0$ se e solo se il numeratore è uguale a $0$. In formule :

$\bigl($ $Supposto$ $denominatore$ $\neq$ $0$ $\bigr)$

$numeratore$ $=$ $0$ $\iff$ $frazione$ $=$ $0$

$Equivalentemente$ :

$numeratore$ $\neq$ $0$ $\iff$ $frazione$ $\neq$ $0$

In riferimento al tuo dubbio, per campo di esistenza intendiamo l'insieme dei valori che possiamo sostituire alle nostre incognite $x$ e per cui abbia senso scrivere una frazione algebrica. Il campo di esistenza risulta essere l'insieme delle $x$ che non annullano il nostro denominatore. Dunque risulterà chiaro che assegnando valori al numeratore non compromettiamo il significato della nostra frazione a patto che siano esclusi quei valori ( come già abbiamo ribadito ) che annullano il nostro denominatore.

Nelle C.E. non ti importa che la frazione sia diversa da 0, ma solo che esista.

Quindi nel tuo caso è sufficiente che sia x - 2 =/= 0  =>  x =/= 2

essendo l'altra ( x^2 + 1 =/= 0 ) automaticamente verificata.

Per x = 0 la frazione esiste e vale zero.