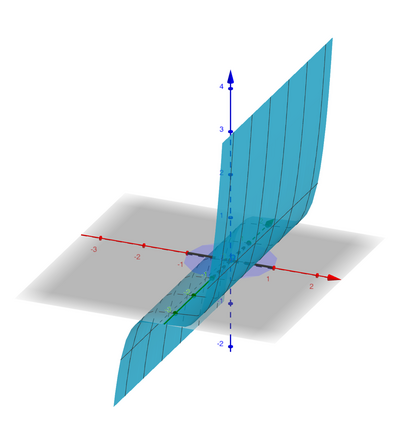
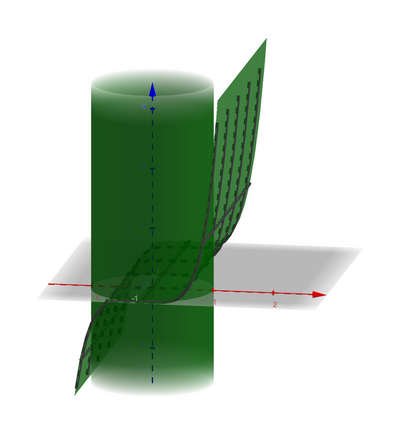
Salve, volevo chiedere: come faccio a capire che l'integrale su D : x^2+y^2<=1
∫ ∫ x^5 dx dy= 0?
Capisco che x^5 è una funzione dispari, ma in base a cosa affermo che l'intervallo è simmetrico?
È una considerazione che faccio nel momento in cui mi isolo la x dalla disequazione x^2+y^2<=1?
148
punti
Livello 1
guarda per bene il grafico di z e ti accorgi che l’asse delle y per z=0 separa la superficie z che definisce il cilindro in due parti aventi volume identico ma di segno opposto.
94654
punti
Genius II
x = r cos t
y = r sin t
0 <= t <= 2pi
0 <= r <= 1
S_[0,2pi] S_[0,1] r^5 cos^5 (t) r dr dt =
= S_[0,1] r^6 dr * S_[0, 2pi] cos^4(t) * cos t dt =
= 1/7 * S_[0, 2 pi ] g(sin t) cos t dt =
= 1/7 * [ G (sin t) ]_[0,2pi] = 0.
g(x) = (1-x^2)^2
47869
punti
Livello 7
94654
punti
Genius II
