Dubbio esercizio trigonometria

Question

Buongiorno ho il seguente problema di trigonometria che ho risolto a metà, nel senso che è il classico problema che mi chiede in prima battuta di determinare la funzione goniometrica (e questo sono riuscito a farlo) e in secondo luogo di risolverla e tracciarne il grafico.

Il mio problema è nella risoluzione di questa equazione. Non saprei da dove partire. Il libro dà come risultato impossibile. L’equazione è:

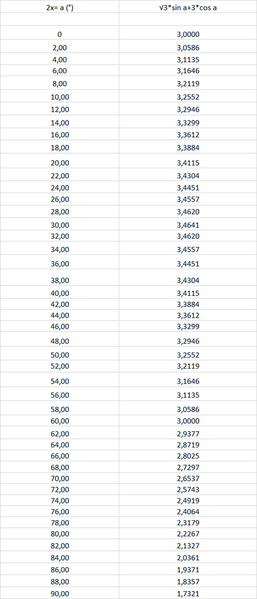
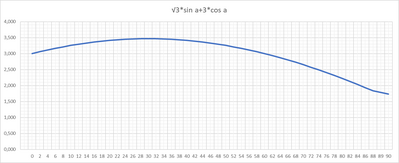
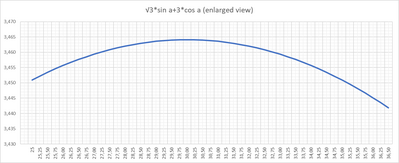
√3sen(2x)+3cos(2x)=9/2.

Grazie come sempre a chi mi aiuterà. Siete un aiuto fantastico!

Autore

Risposta

Max321

(@max321)

83 punti

livello:

Livello 1

38 Risposte
18 1 19

16/03/2024 20:14

Alfonso3 · Accepted Answer

[attach]74751[/attach]

EidosM · Answer

Questa é la classica EQUAZIONE LINEARE in seno e coseno

solo che l'incognita é 2x

Se la traccia é corretta

rad(A^2 + B^2) = rad(3 + 9) = rad 12 = 2 rad 3

C/rad(A^2 + B^2) = 9/2 : (2rad3) = 3 rad(3)/4

é maggiore di 1

e il seno di "2x + a" non può essere questo numero

sin (2x + a) = 3/4 rad 3

é impossibile

EidosM

(@eidosm)

47918 punti

livello:

Livello 7

8502 Risposte
38 3244 1051

16/03/2024 20:22

remanzini_rinaldo · Answer

[attach]74760[/attach] [attach]74758[/attach] [attach]74759[/attach]

exProf · Answer

Con* u = 2*x* c = cos(u)* s = sin(u)* c^2 + s^2 = 1si ha* (√3)*sen(2*x) + 3*cos(2*x) = 9/2 ≡≡ ((√3)*s + 3*c = 9/2) & (c^2 + s^2 = 1) ≡≡ (r ≡ s = - (√3)*(c - 3/2)) & (Γ ≡ c^2 + s^2 = 1)In un riferimento Ocs questo è il sistema dei punti comuni fra la retta r e la circonferenza Γ di raggio uno centrata nell'origine.La distanza di r dall'origine è* |Or| = 3*√3/4 ~= 1.3 > 1quindi la retta è esterna alla circonferenza e, non essendoci punti comuni, l'equazione originaria risulta impossibile.

[Risolto] Dubbio esercizio trigonometria

Domande