Buongiorno volevo sapere se qualcuno mi può aiutare con questa disequazione:
Y=-x^2 +8x - 16
Una volta calcolati tutti i punti (vertice, asse x ecc..) come posso rappresentare questi punti trovati con la parabola sul piano cartesiano? Cioè come faccio a capire in che posizione mettere i vari punti trovati?
20
punti
Livello 0
@zora-bibi quella che hai scritto e’ un’equazione non una disequazione potresti formulare il testo in maniera corretta così ti possiamo aiutare senza fraintendimenti
12909
punti
Livello 7
Basta sostituire i valori trovati nella X, poi ti escono i corrispondenti valori della Y e inserisci i punti nel piano cartesiano. Punti formati dal valore di x inserito e il corrispondente valore di y
23
punti
Livello 0
@ricky_iannu non ho capito molto
Ad esempio, quando trovi l'intersezione con l'asse delle y, imponi x=0 e ti esce y=-16.
Quel -16 lo sostituisci nella y della tua parabola, e risolvi l'equazione -x²+8x-16=-16 e trovi le due x che corrispondono a y=-16
23
punti
Livello 0
@ricky_iannu ok ma il mio professore di matematica ha rappresentato i punti sul piano così:
La mia domanda è come faccio a capire dove mettere i vari punti trovati (vertice, fuoco, asse x, direttrice y) sul piano cartesiano e tracciare la parabola?
Il prof ha appena spiegato la parabola ma non ho capito come tracciarlo in base ai punti trovati e come fare
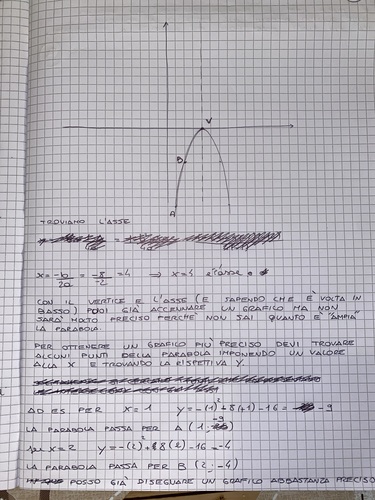
Cara Zora-Bibi, temo che prima dell'aiuto su "come posso rappresentare" ti sia indispensabile "sapere se qualcuno ti può aiutare" con la terminologia.
Quella che tu chiami "questa disequazione" NON LO E' AFFATTO.
Il nome "disequazione" è riservato per indicare un'espressione algebrica contenente uno, ed esattamente uno, operatore relazionale di diseguaglianza aritmetica che sta a separare due subespressioni prive di operatori relazionali dette primo e secondo membro; l'espressione si dice in forma normale canonica se il secondo membro è zero.
---------------
Operatori relazionali di diseguaglianza aritmetica
* "!=" o "<>" o "≠" (si legge "diverso da"); è la diseguaglianza semplice.
* "<=" o "≤" (si legge "minore o eguale a"); è una diseguaglianza d'ordine lasco.
* "<" (si legge "minore di"); è una diseguaglianza d'ordine stretto.
* ">"(si legge "maggiore di"); è l'altra d'ordine stretto.
* ">=" o "≥" (si legge "maggiore o eguale a"); è l'altra d'ordine lasco.
---------------
Le espressioni in cui primo e secondo membro sono separati dall'operatore relazionale d'eguaglianza ("=", si legge "eguale a") hanno il nome "equazione".
==============================
AIUTO SU "come posso rappresentare"
L'espressione fornita
* y = - x^2 + 8*x - 16
è l'equazione di una parabola del piano Oxy con
* asse di simmetria parallelo all'asse y [mancano "y^2" e "x*y"]
* concavità rivolta verso y < 0 [coeff. "a" di x^2 negativo]
Per rappresentare la parabola (con il minimo di operazioni per ogni punto) io consiglio di fare come segue.
---------------
A) Riscrivere l'equazione per evidenziare il vertice V [y = yV + a*(x - xV)^2]
* y = - x^2 + 8*x - 16 ≡
≡ y = - (x^2 - 8*x + 16) ≡
≡ y = - (x - 4)^2
---------------
B) Riconoscere apertura, asse e vertice
* y = - (x - 4)^2 ≡ y = 0 - (x - 4)^2
* apertura a = - 1 < 0
* vertice V(4, 0)
* asse di simmetria x = 4
---------------
C) Calcolare i punti da rappresentare sul piano Oxy come intersezioni di rette perpendicolari all'asse di simmetria
* y = - k (con k > 0)
e opportunamente spaziate (p.es. k = n^2).
Si ha
* - k = - (x - 4)^2 ≡
≡ (x - 4)^2 = k ≡
≡ x - 4 = ± √k ≡
≡ x = 4 ± √k [p.es. x = 4 ± n]
---------------
D) COME RAPPRESENTARE
Lavorare con riga e compasso su carta a quadrettoni.
D1) Tracciare, usando i quadretti: assi (x, y), asse x = 4, vertice V(4, 0).
D2) Per ogni valore di k in {1, 4, 9, 16} [nove punti bastano?] marcare, sulla linea y = - k, i due punti a distanza d = √k sull'asse x = 4.
D3) Con i numeri dell'esempio si hanno i nove punti
* (4, 0), (4 ± 1, - 1), (4 ± 2, - 4), (4 ± 3, - 9), (4 ± 4, - 16)
57382
punti
Genius I
