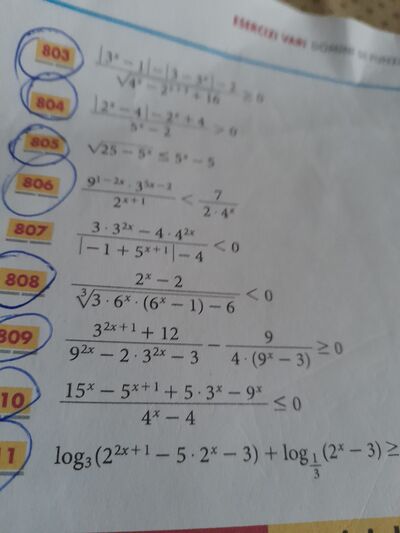Buona serata a tutti; pubblico la disequazione esponenziale n. 807 che, nonostante i ripetuti tentativi, non riesco a risolvere. La risposta è x minore di -1/2 oppure x maggiore di 0. Chiedo gentilmente la spiegazione di tutti i passaggi utili per giungere alla soluzione. Ringrazio anticipatamente chi vorrà aiutarmi.
1502
punti
Livello 1
Una frazione è negativa se e solo se ha termini discordi.
Quindi
807) (3*3^(2*x) - 4*4^(2*x))/(|- 1 + 5^(x + 1)| - 4) < 0 ≡
≡ (3*3^(2*x) < 4*4^(2*x)) & (|- 1 + 5^(x + 1)| > 4) oppure (3*3^(2*x) > 4*4^(2*x)) & (|- 1 + 5^(x + 1)| < 4) ≡
≡ (x > - 1/2) & (x > 0) oppure (x < - 1/2) & (x < 0) ≡
≡ (x > 0) oppure (x < - 1/2)
------------------------------
DETTAGLI
---------------
A) 3*3^(2*x) = 3^(2*x + 1) = 3^u e 4*4^(2*x) = 4^(2*x + 1) = 4^u sono esponenziali di basi diverse con lo stesso esponente u = 2*x + 1 definite, positive e crescenti ovunque con diverse pendenze; pertanto hanno in comune il solo valore uno là dove u = 0, cioè x = - 1/2.
E ciò quali che siano le due basi, dipende solo dall'espressione in x di u.
---------------
B) |- 1 + 5^(x + 1)| = 4 ≡
≡ (- 1 + 5^(x + 1) = - 4) oppure (- 1 + 5^(x + 1) = 4) ≡
≡ (5^(x + 1) = - 3) oppure (5^(x + 1) = 5) ≡
≡ (insieme vuoto) oppure (5^x = 1) ≡
≡ x = 0
57383
punti
Genius I
Ciao grazie mille per la tua risposta. Ti auguro una buona serata: qui è gelida, nebbiosa, tipicamente invernale.
