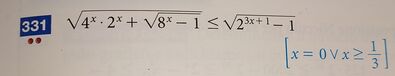[Risolto] Disequazione Esponenziale con radice di radice

CE: x >= 1/3
Soluzione: insieme vuoto.
------------------------------
La condizione di esistenza di un'espressione algebrica è la congiunzione (intersezione ∩, AND, &, ∧) fra le negazioni (complemento, NOT, ¬) di ogni caso che la renda indefinita; in breve, la condizione di esistenza definisce l'insieme di definizione.
Se, com'è per l'esercizio 331, nell'espressione c'è la sola variabile x (intesa reale) l'insieme di definizione è un sottinsieme dell'asse reale x.
------------------------------
L'espressione
331) √((4^x)*2^x + √(8^x - 1)) <= √(2^(3*x - 1) - 1)
essendo composta con operazioni razionali, radici quadrate (cioè potenze) ed esponenziali tutte operazioni definite ovunque non ha condizione d'esistenza: ciascuno dei due membri è definito ovunque nel dominio (asse x) ed ha valore nel codominio (piano di Argand-Gauss).
Ma si tratta di una disequazione con diseguaglianza d'ordine lasco e, mentre l'eguaglianza può avere anche radici complesse, non è così per la diseguaglianza d'ordine stretto che impone la realtà di entrambi i membri: ciò a sua volta impone di risolvere separatamente i due casi e di assumere come soluzione l'unione fra quelle dei casi.
Avendo presente che risolvere per quadrature può introdurre spurie risulta OBBLIGATORIO verificare alla fine la compatibilità con l'espressione originale.
------------------------------
331a) √((4^x)*2^x + √(8^x - 1)) = √(2^(3*x - 1) - 1) ≡
≡ √(8^x + √(8^x - 1)) = √(8^x/2 - 1) ≡
≡ 2*√(8^x - 1) = - (8^x + 2) ≡
≡ 4*(8^x - 1) - (8^x + 2)^2 = 0 ≡
≡ (8^x)^2 - 2*8^x + 8 = 0 ≡
≡ (8^x = 1 - i*√7) oppure (8^x = 1 + i*√7) ≡
≡ (x = log(8, 1 - i*√7)) oppure (x = log(8, 1 + i*√7)) ≡
≡ x = 1/2 ± i*arctg(√7)/ln(8)
ma nessuna delle due radici complesse soddisfà all'originale: sono due spurie.
Resta solo la diseguaglianza d'ordine stretto.
------------------------------
331b) √((4^x)*2^x + √(8^x - 1)) < √(2^(3*x - 1) - 1) ≡
≡ √(8^x + √(8^x - 1)) < √(8^x/2 - 1)
ha senso se e solo se i radicandi sono entrambi non negativi
* (8^x + √(8^x - 1) >= 0) & (8^x/2 - 1 >= 0) ≡
≡ (x >= 0) & (x >= 1/3) ≡
≡ x >= 1/3
quindi
* (√(8^x + √(8^x - 1)) < √(8^x/2 - 1)) & (x >= 1/3) ≡
≡ (insieme vuoto) & (x >= 1/3) ≡
≡ insieme vuoto

8^x - 1 >= 0

2^(3x + 1) - 1 >= 0

significa 8^x >= 1 => x >= 0

3x + 1 >= 0 => x >= -1/3

8^x + sqrt (8^x - 1) <= 2* 8^x - 1

sqrt (8^x - 1) <= 8^x - 1

Posto 8^x - 1 = u con u >= 0

sqrt(u) <= u

u <= u^2

u^2 - u >= 0

u <= 0 oppure u >= 1

8^x - 1 >= 1

8^x >= 2

2^(3x) >= 2

3x >= 1 => x >= 1/3

8^x - 1 <= 0

8^x <= 1 compatibilmente con la prima condizione di esistenza imposta

deve essere 8^x - 1 = 0

8^x = 1 => x = 0