Qualcuno mi può aiutare a risolvere queste dimostrazioni di Geometria?
1) Sia ABC un triangolo. Sulla parallela alla retta BC passante per A considera un punto D, appartenente allo stesso semipiano avente come origine la retta AB a cui appartiene il triangolo, tale che AD=BC. Dimostra che i due triangoli ABC e ADC sono congruenti.
2) Due triangoli ABC e ABD appartengono a semipiani opposti aventi come origine la retta AB e sono tali che AC=BD e BC=AD. Dimostra che AC || BD.
3) Sia ABC un triangolo rettangolo, di ipotenusa BC. Conduci la bisettrice CP e indica con H la proiezione di P su BC. Dimostra che il triangolo ACH è isoscele sulla base AH.
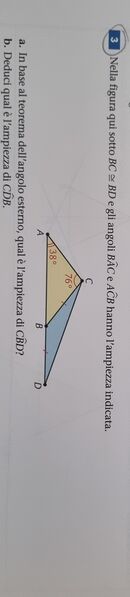
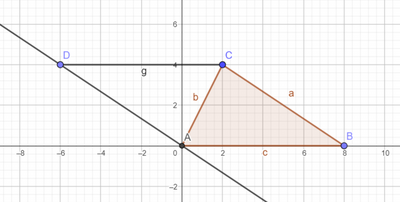
4) vedi immagine