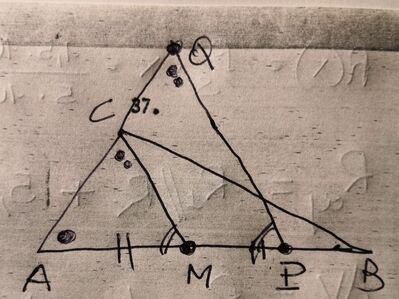
In un triangolo $A B C$, sia $C M$ la mediana uscente da $C$. Considera un punto $P$ sul segmento $M B$ e traccia per $P$ la parallela a $C M$, indicando con $Q$ il punto in cui tale parallela incontra il prolungamento di $A C$. Dimostra che $M B: M P=A C: C Q$.
1
punto
Livello 0
PQ//CM per ipotesi
Dal teorema di Talete:
AM:MP = AC:CQ
Essendo CM mediana del lato AB, i segmenti AM ed MB sono congruenti. Quindi
MB:MP = AC:CQ
76754
punti
Genius II
