Scusate non riesco a svolgere questo problema potreste aiutami.
Grazie mille in anticipo
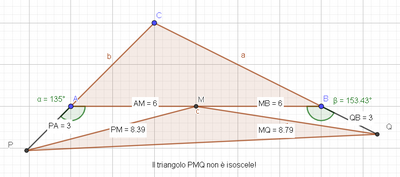
In un triangolo ABC di base AB, prolunga i lati AC e BC rispettivamente dei segmenti AP e BQ congruenti tra loro. Indica M il punto medio della base AB e dimostra che il triangolo PMQ é isoscele.
2
punti
Livello 0
Ciao. Non hai specificato che il triangolo ABC sia ISOSCELE con base AB: solo in tal caso il triangolo PMQ è isoscele. Infatti, l'angolo esterno al triangolo dato in A e l'angolo esterno al triangolo dato in B sono uguali fra loro. Quindi con riferimento ai triangoli APM e MBQ puoi dire che siano congruenti fra loro per il 1° criterio di congruenza dei triangoli : "2 triangoli sono congruenti se hanno 2 lati congruenti fra loro ( e ci siamo!) e l'angolo fra essi compreso (non ci siamo per un triangolo diverso da quello richiesto)"
Quindi non è possibile affermare che PM=MQ che è quanto richiesto dal problema (cioè quanto si debba dimostrare). vedi un esempio grafico:
94774
punti
Genius II
Hp
ACB isoscele
AC=CB
AM=MB
Th
PMQ ISOSCELE
Dim.(AMP),(BMQ)hanno
A=B perché angoli alla base di triangolo isoscele
AP=BQ per diff. di segmenti congruenti (AP=CP-CA),(BQ=CQ-CB)
P=Q perché complementari di triangoli congruenti
i due triangoli sono congruenti per il 1 criterio
MA
P=Q per dim precedente
quindi ne segue che avendo gli angoli alla base congruentj PMQ è isoscele c.v.d
2
punti
Livello 0
