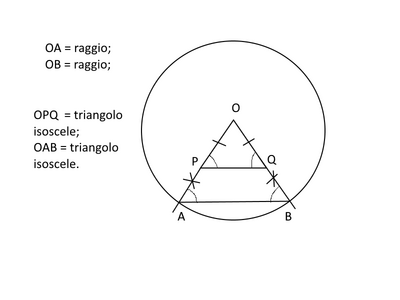
All' interno di un cerchio di centro O, considera due punti PeQ non allineati con O ed equidistanti da O. Detti rispettivamente A e B i punti di intersezione tra le semirette, di origine O,OPeOQ e la circonferenza, dimostra che:
a. i segmenti AB e PQ sono paralleli;
b. il trapezio ABQP è isoscele.
0
punti
Livello 0
Guarda la figura e fai anche tu la costruzione:
I due triangoli OAB e OPQ sono isosceli e simili. Gli angolo alla base sono uguali e corrispondenti, quindi AB e PQ sono lati paralleli.
Il trapezio ABPQ è isoscele, ha le basi parallele, i lati obliqui uguali perchè si ottengono facendo:
raggio - OP;
raggio - OQ;
Op e OQ sono uguali per costruzione; i raggi OA e OB sono uguali.
@cirso ciao.
74863
punti
Genius II
