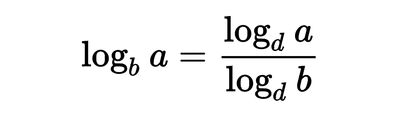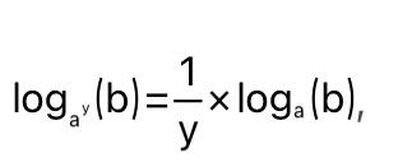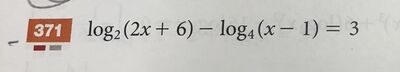Buonasera a tutti,
svolgendo un esercizio sui logaritmi ho utilizzato la formula (1) del cambiamento di base fornita dal mio libro di testo del terzo anno (Matematica.blu 2.0 - Terza edizione),
ovvero (1):
Ma non riesco a trovarmi in nessun modo.
Ho quindi applicato la formula (2), non presente sul mio libro:
e non ho riscontrato difficoltà.
Tuttavia vorrei capire:
- da dove proviene la formula (2), magari con una dimostrazione dettagliata
- perché applicando la formula (1) non riesco ad arrivare al risultato corretto dell’esercizio
Allego foto dell’esercizio in questione:
Risultato: 5
Ringrazio anticipatamente chiunque chiarirà i miei dubbi e mi scuso per non aver fornito un titolo dettagliato in merito al quesito ❤️