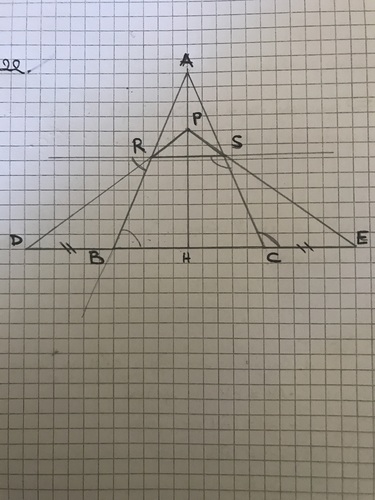
In un triangolo ABC, isoscele sulla base BC, prolunga BC dalla parte di B, di un segmento BD, e dalla parte di C, di un segmento CE, tali che BD è congruente a CE.
considera poi un punto P sull’altezza relativa a BC, e congiungi P con D e P con E. Indica con R il punto di intersezione di PD con AB e con S il punto di intersezione di PE con AC. Dimostra che la retta RS è parallela alla retta BC.
(sopra ho già fatto il disegno)