Difficoltà con problema su fluidi

Question

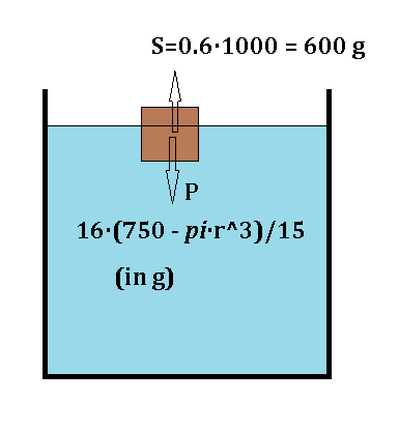
Salve a tutti!Avrei difficolta a risolvere un problema proposto dal docente per esercitarsi in vista dell'esame. Non mi è stato dato né il risultato e né lo svolgimento. Frequento il corso di laurea in Farmacia. Su internet non risulta presente da nessuna parte la soluzione al quesito. Vi ringrazio in anticipo. Il testo è il seguente:Un cubo di legno di lato ℓ =10 cm (d = 800 Kg/m3 ) presenta al suo interno una cavitàsferica vuota. Il cubo posto in acqua galleggia emergendo per 4 cm. Calcolare il raggio dellacavità

LucianoP · Accepted Answer

Il cubo di legno ha volume complessivo:

V=10^3 - 4/3·(pi·r^3) = (1000 - 4·pi·r^3/3) cm^3

d= densità del legno= 800kg/m^3=0.8 kg/dm^3=0.8g/cm^3

Quindi ha una massa pari a

m=(1000 - 4·pi·r^3/3)·0.8 = 16·(750 - pi·r^3)/15 g

Adesso devi pensare che il cubo sia impermeabile all'acqua ed applicare il Principio di Archimede.

Sai andare avanti? Va bene continuo..

16·(750 - pi·r^3)/15 = 600

16·(750 - pi·r^3) = 600·15

12000 - 16·pi·r^3 = 9000

quindi: r = 5·12^(1/3)/(2·pi^(1/3))------> r = 3.907 cm

LucianoP

(@lucianop)

94739 punti

livello:

Genius II

16785 Risposte
5 5753 3465

04/06/2023 16:54

StefanoPescetto · Answer

Indichiamo con x la frazione del volume del cubo piena. Nella situazione di equilibrio il peso del cubo è pari alla spinta di Archimede. I due vettori hanno stessa direzione ma verso opposto.

d_legno *g* (x/100)*V = d_H2O *g*(6/10)*V

x = (6/10)*(10/8) = 3/4 = 75%

Quindi la sfera occupa un volume pari al 25% (1 /4) del volume totale del solido

V_sfera = 250 cm³

R= radice_3 [3*V_sfera /(4*pi)]

Sostituendo i valori numerici otteniamo:

R= 3,9 cm

StefanoPescetto

(@stefanopescetto)

76753 punti

livello:

Genius II

9483 Risposte
0 3970 1882

04/06/2023 17:32

[Risolto] Difficoltà con problema su fluidi

Domande