[Risolto] Determinare la massa di un proiettile

@eugenio

Ciao.

La risoluzione del problema esposto presenta 3 FASI: le prime due ( appena prima dell’urto e subito dopo l’urto) riguardano la quantità di moto del sistema proiettile + pendolo, l’ultima dopo l’urto, l’energia meccanica del sistema complessivo.

1^ FASE

Inizialmente il proiettile possiede una quantità di moto pari a: Q=mv

2^FASE

Riguarda l’urto perfettamente anelastico in cui si conserva la quantità di moto del sistema:

Q = mv = (m+M)*V ove con V si è considerata la velocità del centro di massa del sistema.

Durante queste due fasi l’energia meccanica non si conserva in quanto parte dell’energia si dissipa in calore.

3^FASE

In questa fase si può parlare di conservazione dell’energia meccanica del sistema pendolo+ proiettile. In tale fase abbiamo:

1/2*(m+M)*V^2= energia cinetica immediatamente dopo l’urto

Che si trasforma alla fine tutta in energia potenziale del sistema   (m+M)*g*h

Quindi abbiamo a disposizione nel complesso 2 equazioni:

{ mv = (m+M)*V

{1/2*(m+M)*V^2 = (m+M)*g*h

In queste due equazioni conosciamo:

v = 480 m/s (velocità del proiettile); M=1.8 kg (massa del pendolo); g=9.806 m/s^2 (accelerazione di gravità).

L’altezza h = L·(1 - COS(α)) con L= 1.2 m ed α = 31.4°

Inserendo quindi questi dati nel sistema precedente abbiamo:

{ m·480 = (m + 1.8)·V

{1/2·(m + 1.8)·V^2 = (m + 1.8)·9.806·1.2·(1 - COS(31.4°))

Con uniche incognite m e V. Penso che il più sia fatto. Risolvi il sistema ed ottieni:

m = 0.006988907950 kg ∧ V = 1.856500502 m/s

Quanto richiesto è quindi: m= 7 g peso del proiettile.

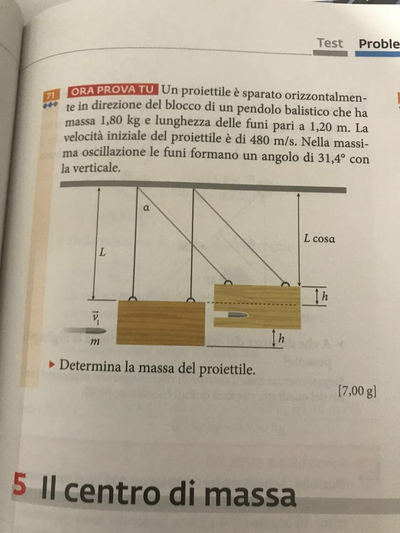
L'urto è anelastico; si conserva la quantità di moto.

Qo = Q1;

Qo è la quantità di moto del proiettile;

Qo = mp * vp = m p * 480. 

(mp = massa del proiettile; M = massa del blocco).

Q1 = (mp + M) * (v blocco),

Il blocco parte con energia cinetica, si solleva di h e acquista energia potenziale (M + mp) * g * h;

h = L - L cos(alfa) = 1,20  - 1,20 * cos(31,4°) = 1,20 - 1,024 = 0,16 m;

1/2 * (M + mp) * (v blocco)^2 = (M + mp) * g * h ;

si semplifica la massa:

v blocco = radicequadrata(2 g h) = radice(2 * 9,8 * 0,16);

v blocco = 1,77 m/s (velocità del blocco dopo l'urto).

Qo = Q1;

mp * 480 = (1,80 + mp) * 1,77;

mp * 480 = 1,80 * 1,77 + mp * 1,77;

mp * 480 - mp * 1,77 = 3,19;

mp * 478,23 = 3,19;

mp = 3,19 / 478,23 = 6,7 * 10^-3 kg = 6,7 grammi; (circa 7 grammi).

Ciao  @eugenio

Riscrivo il testo contrassegnando ogni grandezza con una lettera in modo da poter scrivere una equazione letterale comprensibile !!

Un proiettile è sparato orizzontalmente in direzione del blocco di un pendolo balistico che ha massa M = 1,80 kg e lunghezza delle funi pari a L = 1,20 m. La velocità iniziale del proiettile è di Vp = 480 m/s. Nella massima oscillazione le funi formano un angolo α
di 31,4∘ con la verticale come conseguenza della velocità Vb acquisita dal blocco .

Determina la massa m del proiettile

Si conserva la  Q. di M. del proiettile , vale a dire 

m*Vp = (M+m)*Vb 

dalla equazione Vb^2 = 2gh si ricava Vb nel seguente modo :

h = L-L*cos α = L(1-cos α) = 1,20*(1-cos 31,4°) = 1,20*(1-0,8536) = 0,176 m (la quantità MA dello sketch sottostante)

Vb = √2*9,806*0,176 = 1,857 m/sec 

ed infine :

m*Vp-m*Vb =  M*Vb

m(Vp-Vb) = M*Vb

m = M*Vb / (Vp-Vb) = (1,80*1,857) / (480-1,857) = 0,0070 kg (7,0 grammi)