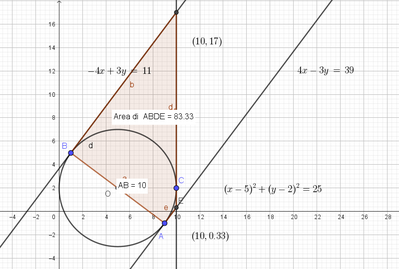
Scrivi l'equazione della circonferenza circoscritta al triangolo di vertici $A(9 ;-1), B(1 ; 5)$ e $C(10 ; 2)$. Tracciate le tangenti alla circonferenza nei punti $\mathrm{A}, \mathrm{B}, \mathrm{C}$ e detti $D$ ed $E$ i loro punti di intersezione, trova il perimetro e l'area del quadrilatero non intrecciato $A B D E$ formato dalle tangenti e dal segmento $A B$.
Salve! Qualcuno mi potrebbe aiutare che non capisco che se ci sono tre rette tangenti alla circonferenza come viene D e E i loro punti di intersezione? Non dovrebbe venire 3 ?
Sono riuscita a trovare soltanto l’equazione della circonferenza