Ciao, ho un problema di geometria che non riesco proprio a risolvere.
Lo scrivo di seguito. Ringrazio chi saprà aiutarmi.
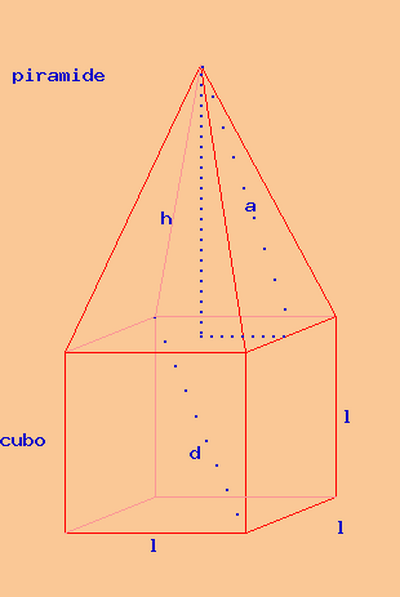
Un solido formato da un cubo sormontato da una piramide con la base coincidente con una faccia del cubo; sapendo che l'area totale del solido è 3840 cm² e che lo spigolo del cubo è 6/5 dell'apotema della piramide, calcola il volume e il peso del solido sapendo che il Ps è 2,5.
Grazie ancora