Crescita batterica nei prodotti alimentari

@sussannati

Ciao e benvenuta

R: poco più di 6 giorni

Infatti la funzione è: y = 200·e^(0.5·t)

Devi porre: y = 5000 (milioni)

5000 = 200·e^(0.5·t)----> e^(t/2) = 25

quindi: t = 4·LN(5)-----> t = 6.4378 giorni

5*10^3/200 = e^0,5t

25 = e^0,5t

ln 25 = 0,5t*ln e 

poiché ln e = 1 , si ha : 

t = 2*ln 25 = 6,44 gg

SETTE GIORNI
* 200*e^(t/2) >= 5000 ≡
≡ e^(t/2) >= 5000/200 = 25 = 5^2 ≡
≡ ln(e^(t/2)) >= ln(5^2) ≡
≡ t/2 >= 2*ln(5) ≡
≡ t >= 4*ln(5) ~= 6.4 g
e il minimo numero intero di giorni superiore a sei e mezzo è sette.

DOPO CINQUE GIORNI IL PRODOTTO VA IN "OFFERTA DEL GIORNO" DI MODO CHE LA SOGLIA SIA SUPERATA NEL FRIGORIFERO DEL CLIENTE E NON IN QUELLO DEL NEGOZIO.

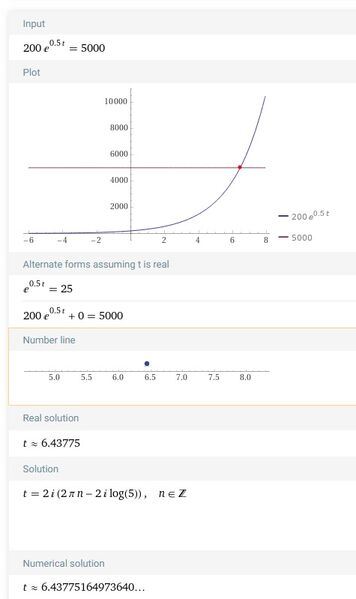
La crescita batterica nei prodotti alimentari rende necessaria la data di scadenza per alcuni prodotti, affinchè siano venduti e consumati prima che la carica batterica sia troppo alta. Si supponga che per un dato prodotto, la crescita batterica sia descritta dalla funzione: f(t)=200e0.5t, dove t misura il numero di giorni trascorsi dall'inscatolamento del prodotto e f(t) è espresso in milioni di individui.

Sapendo che un prodotto non può essere consumato in sicurezza se la carica batterica raggiunge i 5000 milioni di individui, si stabilisca quanto tempo dopo l'inscatolamento il prodotto non sarà considerato sicuro.

.........................

https://www.wolframalpha.com/input?i=200*e%5E%280.5*t%29+%3D+5000

e^(0.5 t) = 25 ---> 0.5*t = ln25 ---> t = ln625  ---> t = 6.43775... giorni

oppure se f(t) è espresso in "individui"...