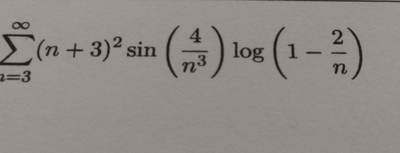Salve a tutti, sto cercando di risolvere questo esercizio:
La serie $\sum_{n=3}^{∞<}{(n+3)^2 sen(\frac{4}{n^3}) log(1 - \frac{2}{n})}$
a) diverge a +∞
b) converge a un numero positivo
c) converge a un numero negativo
d) diverge a -∞
Ho calcolato il $\lim_{x\to ∞ }{a_n}$ che come risultato da 0, dunque so che potrebbe convergere.
Ho pensato di usare il confronto asintotico e riscrivere $a_n$ come:
$n^2 (\frac{4}{n^3}) (1- \frac{2}{n})$ ma non so se il ragionamento è giusto, qualcuno può darmi un suggerimento?
Grazie in anticipo.