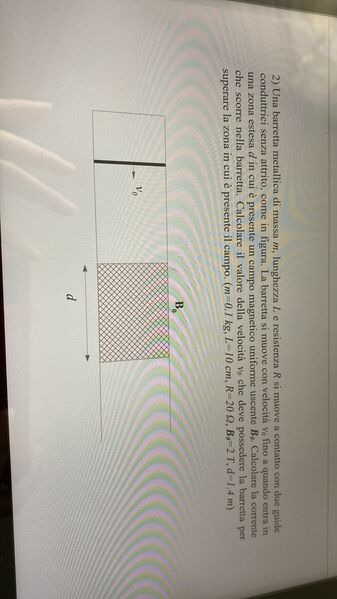
Una barretta metallica di massa $m$, lunghezza $L$ e resistenza $R$ si muove a contatto con due guide conduttrici senza attrito, come in figura. La barretta si muove con velocità $v_{0}$ fino a quando entra in una zona estesa $d$ in cui è presente un campo magnetico uniforme uscente $B _{0}$. Calcolare la corrente che scorre nella barretta. Calcolare il valore della velocità $v_{0}$ che deve possedere la barretta per superare la zona in cui è presente il campo. $\left(m=0.1 kg , L=10 cm , R=20 \Omega, B_{0}=2 T, d=1.4 m\right)$
Esercizio di fisica