In una circonferenza di centro $O$ e raggio lungo $65 cm$, le due corde $A B$ e $B C$ misurano rispettivamente $120 cm$ e $78 cm$. Chiama $M$ e $N$ rispettivamente i punti medi di $A B$ e di $B C$.
Calcola il perimetro e l'area del quadrilatero MBNO.
per favore nn so come farlo pls
11
punti
Livello 0
Ciao e benvenuto. Con riferimento alla figura allegata, considero i triangoli: OMA ed ONC
Essi sono triangoli rettangoli. Per essi applico il teorema di Pitagora:
AM=MB=60 cm---------> OM=√(OA^2 - AM^2) =√(65^2 - 60^2) = 25 cm
CN=BN= 39 cm--------->ON=√(OC^2 - NC^2) =√(65^2 - 39^2) = 52 cm
Quindi :
perimetro=OM+MB+BN+ON=25 + 60 + 39 + 52= 176 cm
area=MB*MO/2+BN*ON/2=60·25/2 + 39·52/2 = 1764 cm^2
94774
punti
Genius II
OM = 5√13^2+12^2 = 5*5 = 25
ON = 13√5^2-3^2 = 13*4 = 52 cm
perim . 2p = 60+25+52+39 = 176 cm
area A = (60*25+39*52)/2 = 1.764 cm^2
114465
punti
Genius II
@remanzini_rinaldo Grazie, Rinaldo, ottimo lavoro anche il tuo, come sempre del resto!
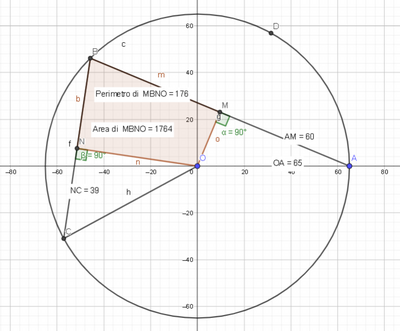
Disegna la circonferenza con centro O con raggio r= 65 cm;
traccia la corda AB= 120 cm;
traccia la corda partendo da B toccando la circonferenza in C con lunghezza BC= 78 cm;
segna i punti medi delle corde con M per AB e con N per BC;
quindi i lati del quadrilatero MBNO risulteranno:
MB= 120/2 = 60 cm;
BN= 78/2 = 39 cm;
per il lati OM e NO applica il teorema di Pitagora ai triangoli rettangoli OMB e NOB come segue:
OM= √[65²-(120/2)²] = √[65²-60²] = 25 cm;
NO= √[65²-(78/2)²] = √[65²-39²] = 52 cm;
risultati:
perimetro MBNO 2p= MB+BN+OM+NO = 60+39+25+52 = 176 cm;
area MBNO A= (60×25+52×39)/2 = 1764 cm² (cioè la somma delle aree dei triangoli rettangoli OMB e NOB).
57950
punti
Genius I
@gramor ...ottimo lavoro, Graziano !!! Felice Domenica
