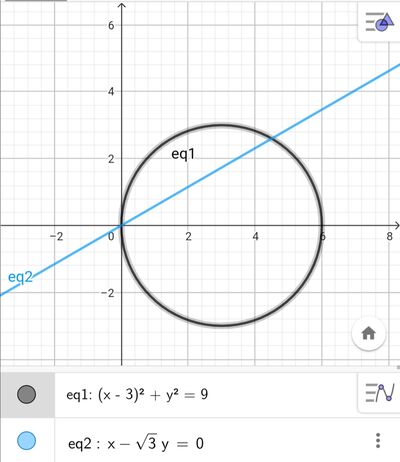
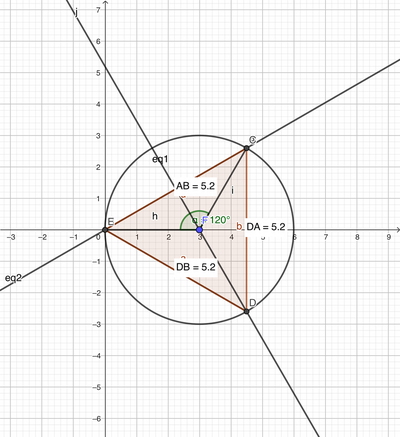
Data la circonferenza di equazione $x^2+y^2-6 x=0$ e la retta di equazione $x-y \sqrt{3}=0$ :
a) verifica che la retta stacca sulla circonferenza una corda di misura uguale a quella del lato di un triangolo equilatero inscritto nella circonferenza;
b) determina l'area del minore dei due segmenti circolari limitati dalla circonferenza e dalla corda di cui al punto a.
a. $2 \sqrt{3} ;$ b. $\left.3 \pi-\frac{9 \sqrt{3}}{4}\right]$
20
punti
Livello 0
a) scriviamo la risolvente di
{ x^2 + y^2 - 6x = 0
{ x = y rad 3
y = x/rad 3
x^2 + x^2/3 - 6x = 0
4/3 x^2 - 6x = 0
D = b^2 - 4 a c = 6^2 = 36
AB = rad (D*(1+m^2))/|a| = rad(36)* rad(1 + 1/3)/(4/3) = 6*3/4 * rad(4/3) =
= 9/2*2/rad 3= 3 rad 3 = r rad 3
essendo
x^2 - 6x + 9 + y^2 = 0
(x - 3)^2 + y^2 = 3^2
e quindi r = 3
b) il settore circolare corrispondente ha area Ss = pi * 120/360 * 3^2 = 3 pi
mentre il triangolo che va sottratto ha base 3 rad 3 ed altezza
h = rad (3^2 - (3/2*rad(3))^2) = rad (9 - 27/4) = rad(9/4) = 3/2
St = 1/2 * 3 rad(3) * 3/2 = 9/4 rad 3
S = Ss - St = 3 pi - 9/4 rad 3 = 3 (pi - 3/4 rad 3)
47893
punti
Livello 7
Circonferenza di centro C(3;0) e raggio R =3
(x-3)²+y²=9
La distanza del centro dalla retta data è il cateto di un triangolo rettangolo avente come ipotenusa il raggio e come altro cateto metà corda. La distanza centro retta è
d= 3/radice (1+3)=3/2
Quindi metà corda ha lunghezza:
L= radice (3² - 9/4) = radice (27/4) = (3/2)*radice (3)
La corda intercettata ha quindi lunghezza doppia, 2L=3*radice (3) = R*radice (3) ok
L'angolo al centro sotteso dalla corda è doppio del corrispondente angolo alla circonferenza (60°=Angolo triangolo equilatero)
Determino l'area del segmento circolare come differenza tra l'area del settore circolare di ampiezza 120° e l'area del triangolo isoscele di cui abbiamo precedentemente trovato base(corda) e altezza (distanza dal centro)
A=(1/3)*pi*9 - (9/4)*radice (3) = 3*pi - (9/4)*radice (3)
76753
punti
Genius II
94726
punti
Genius II
