Buongiorno. Ho provato a svolgere l’esercizio seguente.
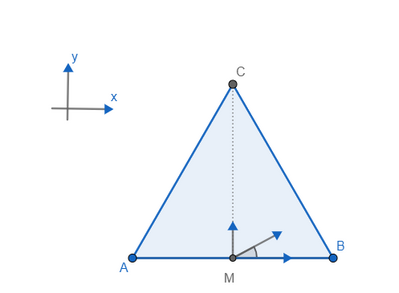
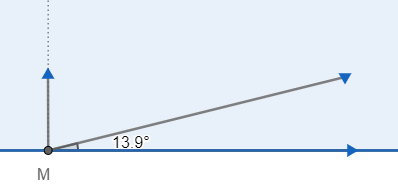
Tre cariche puntiformi $q_A=-q_B$ e $q_C=3 \mu \mathrm{C}$ sono poste nei vertici $A, B$ e $C$ di un triangolo equilatero di lato $l=1 \mathrm{~m}$. Una quarta carica puntiforme $q_H$ è posta nel punto medio $\mathrm{H}$ del segmento $A B$ e subisce una forza di modulo pari a $0,740 \mathrm{~N}$, che forma un angolo $\theta=14^{\circ}$ con la direzione dell'asse $x$ positivo, su cui giace $A B$. Determinare il valore della carica $q_H$. Si usi il valore $k=8.99 \times 10^9 \mathrm{~N} \mathrm{~m}^2 \mathrm{C}^{-2}$ per la costante di Coulomb.
Allego alcuni calcoli che ho fatto. Spiego come ho ragionato perché i miei calcoli sono scritti male. La forza che agisce sulla carica QH avrò una componente x è una componente y. La carica qua e la carica QB applicano una forza su cucca che ha solo la componente x. Quindi lungo l’asse X avrò che la forza su QH sarà la somma della forza di QA lungo il versore i + la forza della carica Qb lungo il versore -i. Invece sull’asse Y agisce solo la carica QC lungo il versore -j. E da questo dovrei ricavarmi QH.. è corretto?