Salve, potreste aiutarmi con questo esercizio?
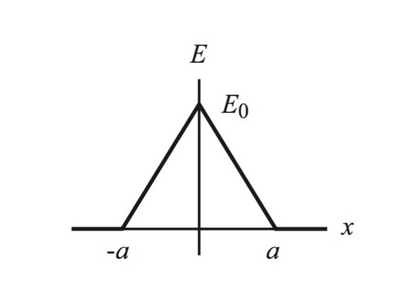
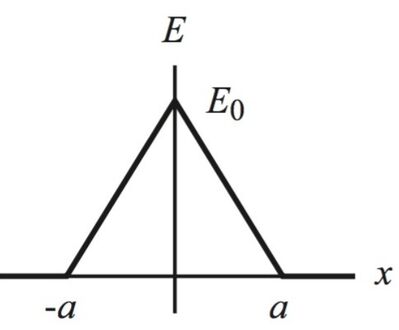
Determinate l’espressione analitica ed il grafico della densit`a volumetrica di carica ρ
e del potenziale elettrico φ associati al campo elettrico mostrato in figura. Il campo
elettrico `e indipendente dalle coordinate y ed z. Assumete inoltre che φ = 0 nel punto
x = 0.
...............................
è
per x >0 Ex(x) = - Eo*x/a + Eo = Eo(1 - x/a)
e
per x < 0 Ex(x) = Eo*x/a + Eo = Eo(1 + x/a)
flusso di E = intg-triplo di rho dV
o a livello differenziale divE = rho/eps0
∂Ex/∂x + ∂Ey/∂y + ∂Ez/∂z = rho/eps0
dalle ipotesi:
per x > 0
-Eo/a = dE/dx = ∂Ex/∂x + ∂Ey/∂y + ∂Ez/∂z = ∂Ex/∂x + 0 + 0 = rho/eps0 ---> rho(x) = eps0*(-Eo/a) ---> costante negativa
per x < 0
Eo / a = dE/dx = ∂E/∂x + ∂E/∂y + ∂E/∂z = ∂E/∂x + 0 + 0 = rho/eps0 ---> rho(x) = eps0*(Eo/a) ---> costante positiva
il potenziale phi(x) è definito da:
E = - grad phi = - (∂phi/∂x *i + ∂phi/∂y * j + ∂phi/∂z * k)
e qui
E = - grad phi = - (∂phi/∂x *i + ∂phi/∂y * j + ∂phi/∂z * k ) = - (∂phi/∂x *i + ∂phi/∂y * j + ∂phi/∂z * k ) = - ∂phi/∂x *i = - dphi/dx *i
quindi:
dphi/dx = Ex ---> dphi = Ex*dx ---> phi(x) = intg Ex*dx + cost
per x > 0
phi(x) = intg(da 0 a x) Eo(1 - x/a)dx = Eo ( x - x²/(2a))
per x < 0
phi(x) = intg(da 0 a x) Eo(1 + x/a)dx = Eo ( x + x²/(2a))
... controlla.