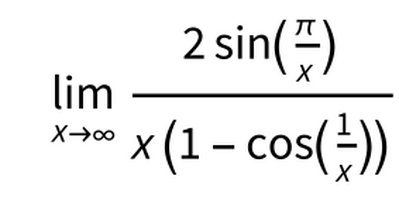Buonasera, sto provando a risolvere questo esercizio.
Ho posto 1/x =y e riscritto il limite:
lim (2 y sin (pi*y))/(1-cosy) = 0/0 F.I.
y->0
Per cui ho applicato il teorema di de l'Hopital ottenendo:
lim (2 pi sin(pi*y) + 2 pi y cos(pi*y))/(1+siny) = 0/1 = 0
y->0
Il risultato però riporta 4pi. Vorrei capire cosa sbaglio.
Grazie
229
punti
Livello 1
Posto, come hai fatto tu, t = 1/x
quando x->oo, t -> 0
lim_t->0 2 sin (pi t)/[1/t * (1 - cos t ) ] =
divido num e den per t e poi al numeratore moltiplico e divido per pi
= lim_t->0 2 pi (sin pi t)/(pi t) / ((1 - cos t )/t^2 )
spezzo in tre parti
2 pi lim_(pi t -> 0) sin (pi t)/(pi t) : lim_t->0 (1 - cos t)/t^2
e usando i limiti notevoli
2 * 1 * pi / (1/2) = 4 pi
47869
punti
Livello 7
