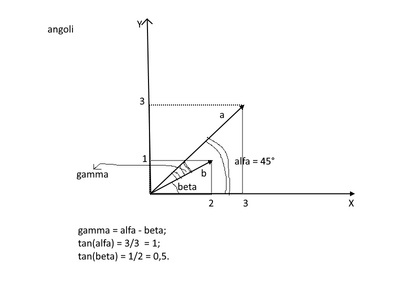
Il modulo di a dovrebbe essere pari a 4.24 e quello di b a 2.24 motivo per cui, utilizzando la formula cos(x) = vx/|v| sia per il primo che per il secondo vettore, ho ottenuto rispettivamente 45° e 26.8°. I risultati dovrebbero essere 45° e 16.56° la cui differenza, che ci dà l'angolo richiesto, risulta 18.44°. Come mai ottengo un risultato diverso?
265
punti
Livello 1
N. B. Avrei voluto scrivere a=3x+3y
a = 3x + 3y;
b = 2x + 1y.
tan (alfa) = y / x = 3/3 = 1;
alfa = arctan(1) = 45° , (angolo che a forma con l'asse x);
tan(beta) = 1/2;
beta = arctan(0,5) = 26,565°, (angolo che b forma con l'asse x).
angolo gamma fra i due vettori:
gamma = alfa - beta = 45° - 26,565° = 18,443° = 18,44°.
Mi sembra possa andare.
I moduli dei vettori non servono se usi la tangente:
tan(angolo) = (cateto opposto) / (cateto adiacente).
Modulo di a:
a = radice(3^2 + 3^2) = radice(18) = 4,243;
modulo di b:
b = radice(2^2 + 1^2) = radice(5) = 2,236 = 2,24.
ciao @mirea00
74783
punti
Genius II
NON CRUCCIARTI, ANCHE "risulta 18.44°" E' UN ERRORE (dovrebb'essere 18.43°).
------------------------------
Io i vettori preferisco scriverli ELENCANDO LE componenti (coordinate della punta se la cocca è nell'origine) piuttosto che SOMMANDO I componenti (la componente per il versore è il componente), cioè per me
* a = 3*x + 3*y ≡ a(3, 3) oppure A(3, 3) se voglio evidenziare la punta
* b = 2*x + y ≡ b(2, 1) oppure B(2, 1)
---------------
Il quesito chiede di calcolare l'angolo θ fra i due vettori (a, b), cioè chiede di calcolare il prodotto scalare nei due modi e di eguagliare le due espressioni.
Come "scontrino di supermercato" il prodotto scalare è la somma dei prodotti fra le componenti omologhe
* a.b = (3, 3).(2, 1) = 3*2 + 3*1 = 9
Come "correttivo a Pitagora" il prodotto scalare è il prodotto fra i moduli dei vettori e il coseno dell'angolo che formano
* a.b = |(3, 3)|*|(2, 1)|*cos(θ) = (3*√2)*(√5)*cos(θ) = (3*√10)*cos(θ)
quindi
* cos(θ) = 9/(3*√10) = 3/√10
* θ = arccos(3/√10) ~= 0.32 ~= 18° 26' 5.8''
57382
punti
Genius I
