Ciao riuscite a darmi una mano con questo esercizio per favore
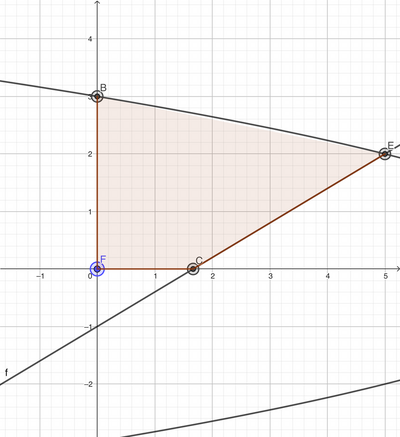
Calcola il volume del solido generato dalla rotazione completa attorno all'asse y del trapezoide individuato dalla porzione di parabola di equazione x = 9 - y ^ 2 contenuta nel semipiano positivo delle y, l'asse y e dalla retta di equazione y = 3/5 x - 1.
87
punti
Livello 1
Ma non l’avevo già risolto?
Punto E (grafico)
{x = 9 - y^2
{y = 3/5·x - 1
risolvi ed ottieni:[ x = 5 ∧ y = 2 , x = - 40/9 ∧ y = - 11/3 ]
Scarti la seconda
Espliciti la retta in x:
x = 5·y/3 + 5/3
Lavori per integrazione.
∫(pi·(5·y/3 + 5/3)^2 )dy=25·pi·(y + 1)^3/27
25·pi·(2 + 1)^3/27 = 25·pi
25·pi·(0 + 1)^3/27 = 25·pi/27
25·pi - 25·pi/27 = 650·pi/27
poi
∫(pi·(9 - y^2)^2) dy= pi·y·(y^4 - 30·y^2 + 405)/5
pi·3·(3^4 - 30·3^2 + 405)/5 = 648·pi/5
pi·2·(2^4 - 30·2^2 + 405)/5 = 602·pi/5
648·pi/5 - 602·pi/5 = 46·pi/5
Sommi i due risultati:
650·pi/27 + 46·pi/5 = 4492·pi/135
94802
punti
Genius II
