@lukegemini
Ciao di nuovo.
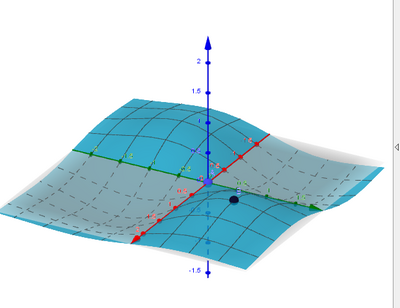
z = x·y·e^(- (x^2 + y^2)/2)
Applico le C.N.:
{Z'x=0
{Z'y=0
che si traducono nel sistema:
{y·e^(- x^2/2 - y^2/2) - x^2·y·e^(- x^2/2 - y^2/2) = 0
{x·e^(- x^2/2 - y^2/2)·(1 - y^2) = 0
Lo risolvo ed ottengo 5 punti critici:
[x = 0 ∧ y = 0, x = 1 ∧ y = 1, x = 1 ∧ y = -1, x = -1 ∧ y = 1, x = -1 ∧ y = -1]
In corrispondenza di ciascuno di essi valuto l'Hessiano H(x,y):
|Z''xx..........Z''xy|
|Z''yx..........Z''yy|
quindi considero le C.S. per stabilire la natura del punto critico trovato
Z''xx=x·y·e^(- x^2/2 - y^2/2)·(x^2 - 1) - 2·x·y·e^(- x^2/2 - y^2/2)
Z''yy=x·y·e^(- x^2/2 - y^2/2)·(y^2 - 3)
Z''xy=Z''yx=e^(- x^2/2 - y^2/2)·(x^2·(y^2 - 1) - y^2 + 1)
Ottengo:
H(0,0)= -1<0-----------> (0,0) è un punto di sella
|0........1|
|1........0|
H(1,1)= 4e^(-2)>0, Z''xx=-2e^(-1)<0
|-2e^(-1).........0|
|0.........-2e^(-1)|
Quindi (1,1) è un punto di max relativo
H(1,-1)=H(-1,1) =4e^(-2) >0--------->(1,-1), (-1,1) punti di minimo relativo
|2e^(-1)........0|
|0........2e^(-1)|
essendo Z''xx>0
H(-1,-1)= 4 e^(-2), Z''xx=-2e^(-1)<0
|-2e^(-1)..........0|
|0..........-2e^(-1)|
Quindi, (-1,-1) punto di max relativo (come (1,1))