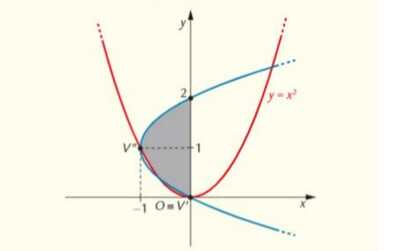
34 Con riferimento alla figura, rispondi ai seguenti quesiti:
a. inscrivi nel segmento parabolico limitato dalla parabola di equazione $y=x^{2}$ e dalla retta di equazione $y=4$ il rettangolo di perimetro massimo avente due lati paralleli all'asse $y$
Salve, avrei bisogno di sapere come procedere per risolvere il primo punto del seguente problema (solo il primo). Grazie
9
punti
Livello 0
I due lati paralleli all'asse y, sulle rette
* x = ± k, con 0 < k < 2
sono lunghi
* 4 - k^2
e i due lati paralleli all'asse x, sulle rette y = 4 e y = k^2 sono lunghi
* 2*k
quindi il perimetro da massimizzare è
* p(k) = 2*(4 - k^2 + 2*k) = - 2*((k - 1)^2 - 5) = 10 - 2*(k - 1)^2
questa è l'equazione, nel piano Okp, di una parabola còncava in basso (apertura - 2 < 0) e con vèrtice V(1, 10).
Quindi il rettangolo inscritto di massimo perimetro lo si ottiene per k = 1, con p(1) = 10.
Vedi al link
http://www.wolframalpha.com/input/?i=2*%284+-+k%5E2+%2B+2*k%29+where+k%3D1
57382
punti
Genius I
Grazie mille!!!
