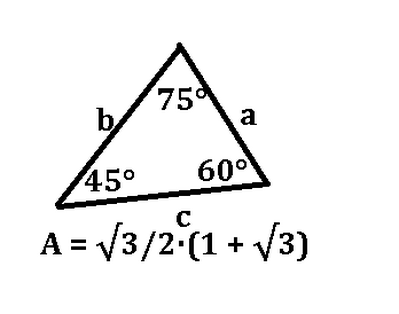Buon pomeriggio, non riesco a capire questo esercizio di Trigonometria:
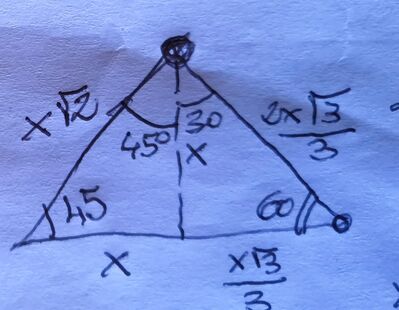
"In un triangolo l'area misura √3/2 (1+ √3) e due angoli hanno ampiezze π/4 e e π/3. Calcola le misure degli altri elementi al triangolo".
Soluzione: [5/12 π; 2, √6, √3+1]
Finora purtroppo sono riuscita a trovare solo il terzo angolo e per il resto sono arenata. Grazie mille in anticipo!
10
punti
Livello 0
In un triangolo rettangolo avente angoli acuti di 30 e 60 gradi il cateto opposto all'angolo di 30 gradi è metà dell'ipotenusa e il cateto maggiore, opposto all'angolo di 60 gradi è uguale al cateto minore per radice (3)
Un triangolo rettangolo avente angoli acuti di 45° è equivalente alla metà di un quadrato avente lato congruente con la lunghezza dei cateti. L'ipotenusa del triangolo rettangolo è la diagonale del quadrato (L*radice 2)
76753
punti
Genius II
@stefanopescetto ti ringrazio della risposta, mi è abbastanza chiara e penso di aver capito. Provo a rifarlo seguendo il tuo procedimento. Ti auguro una buona serata.
Angolo incognito:
pi - (pi/4 + pi/3) = 5·pi/12
Tradotti in gradi sessagesimali sono pari a quelli di figura di sopra.
Teorema dei seni con i lati a e b:
a/SIN(45°) = b/SIN(60°)----> √2·a = 2·√3·b/3
quindi: a = √6·b/3
Si ha poi:
Α = 1/2·a·b·SIN(75°) = √3/2·(1 + √3)
Α = 1/2·(√6·b/3)·b·SIN(75°)-----> Α = b^2·(√3/12 + 1/4)
b^2·(√3/12 + 1/4) = √3/2·(1 + √3)
b = - √6 ∨ b = √6
a = √6·√6/3-----> a = 2
ancora teorema dei seni:
c/SIN(75°) = a/SIN(45°)--->c·(√6 - √2) = √2·a
c·(√6 - √2) = √2·2----> c = √3 + 1
94739
punti
Genius II
@lucianop grazie mille, volevo capire meglio il passaggio da "Si ha poi" perché mi è abbastanza chiara la sostituzione di b ma poi non ho capito il passaggio successivo. Grazie in anticipo e buona serata.
Vertici: A, B, C
Piede su AB dell'altezza da C: H
Angoli: α = π/4, β = π/3, γ = π - (π/4 + π/3) = 5*π/12
Quindi
* AHC è metà quadrato di lato |AH| = |HC| = h e diagonale |AC| = h*√2
* HBC è metà triangolo isoscele di altezza |HC| = h, lato |BC| = L = h/(√3/2), semilato |HB| = L/2 = h/√3
da cui
Lati: |AB| = |AH| + |HB| = h*(1 + 1/√3), |AC| = h*√2, |BC| = 2*h/√3
Area: |AB|*|HC|/2 = (1 + 1/√3)*h^2/2 = (√3/2)*(1 + √3) ≡
≡ h = √3
Infine
* |AB| = (√3)*(1 + 1/√3) = (√3 + 1)
* |AC| = h*√2 = √6
* |BC| = 2*h/√3 = 2
NON M'E' SEMBRATO AFFATTO "un esercizio di Trigonometria".
57382
punti
Genius I
@exprof ti ringrazio. La mia prof me lo aveva assegnato come esercizio di Trigonometria e infatti è nel capitolo "Trigonometria" del libro "Matematica.azzurro 4". Devo ragionare ancora un po' ma non sono molto lontana dal capirlo. Ancora buona serata.
@annae_labyrinthus e p.c. @StefanoPescetto @LucianoP
Non trovi contraddittorio scrivermi "ti ringrazio" e clickarmi un cuorinfranto senza dirmene il motivo? Se tu fossi stata un maschietto t'avrei detto che quel click è stato un riflesso uterino, ma a una femminuccia non lo posso dire.
Definizione: un problema è "di Trigonometria" se e solo se non lo si possa risolvere senza usare almeno un concetto di Trigonometria.
Non è il caso in esame: nella mia soluzione ho usato solo algebretta e geometria euclidea.
Che sia «nel capitolo "Trigonometria" del libro "Matematica.azzurro 4"» conferma la mia pessima opinione delle attuali direttive sull'adottabilità dei testi e sui testi medesimi.
Che la tua prof te l'avesse assegnato «come esercizio di Trigonometria» conferma la mia pessima opinione sui colleghi che assegnano problemi senza prima averli risolti loro.
Buona serata anche a te, e in futuro motiva i tuoi click.
@exprof chiedo scusa per il click errato, dato che volevo mettere un like ma dopo l'errore mi diceva "hai già votato questo elemento"; ho provato a eliminare ma non sono riuscita. Avrei preferito una risposta più rispettosa, dal momento che è possibile anche un errore di digitazione e non è necessario "adirarsi" per una questione di definizione: infatti non avendo grandi competenze in materia mi sono affidata a ciò che mi aveva detto la mia insegnante. Preferirei un tono meno "cattedratico" e più dialogante, dal momento che questa piattaforma è fatta per diffondere conoscenza e non per accusare di ignoranza nessuno. Detto ciò, le auguro ancora una buona serata.
