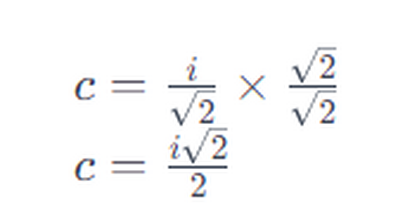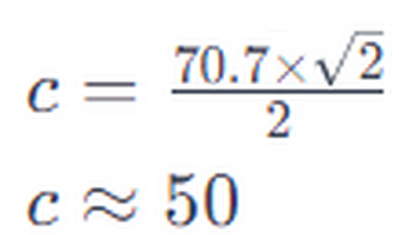Angolo di $45^{\circ}$
Il segmento PA è tangente alla circonferenza di centro 0 . Utilizzando i dati riportati in figura, calcola il perimetro e l'area del triangolo AOP. $\quad\left\{170.7 \mathrm{~cm} ; 1250 \mathrm{~cm}^2\right\}$
Buonasera, qualcuno che potrebbe darmi un aiuto con esercizio 172?
Grazie mille a chi saprà dirmi!
103
punti
Livello 1
Il triangolo AOP è un triangolo rettangolo isoscele perché:
Angolo P = 45°
Angolo A = 90 °
Angolo O = 180 - (90+45) = 180 - 135 = 45°
Risulta un triangolo rettangolo isoscele perché ha 2 angoli uguali a 45° e un angolo retto 90°.
Di conseguenza i lati AO = AP, rappresentano i cateti mentre PO è l'ipotenusa;
i = PO = 70,7 cm (ipotenusa)
Essendo: c = AO =OP (cateti)
Applico Teorema di Pitagora:
applico la formula inversa e ricavo i cateti:
Quindi
Abbiamo:
c = AO = AP = 50 cm
OP = 70,7 cm
Perimetro
P = 50 + 50 + 70,7 = 170,7 cm
Area
A = (AO*AP)/2 = (50*50)/2 = 2500/2 =1250 cm2
5968
punti
Livello 6
@casio 👍👍
=================================================
$AP = OA = \dfrac{OP}{\sqrt2} = \dfrac{70,7}{1,414} = 50\,cm;$
perimetro $2p= AP+OA+OP = 50+50+70,7 = 170,7\,cm;$
area $A= \dfrac{50^2}{2} = \dfrac{2500}{2} = 1250\,cm^2.$
57816
punti
Genius I
@gramor 👍👍
OP è la diagonale di un quadrato di lato AO(AP)
AO = AP = 70,7*0,707 = 50,0 cm
perimetro 2p = 100+70,7 = 170,7 cm
area A = 50^2/2 = 1250 cm^2
114196
punti
Genius II
c=i/radquad2=70,7/1,414=50 A=50*50/2=1250cm2 Peri,.=100+70,7=170.7cm
9850
punti
Livello 7
