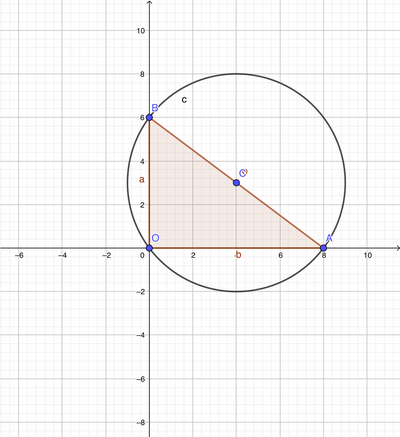
Considera la circonferenza di equazione x^2+y^2-8x-6y=0. Siano C il suo centro , A il punto (di ascissa non nulla) di intersezione con l'asse delle ascisse e B quello (con ordinata non nulla) con l'ascissa delle ordinate. Verifica che A,B e C sono allineati
95
punti
Livello 0
Possiamo riscrivere l'equazione della circonferenza:
(x-4)² + (y-3)² = 25
Quindi l'equazione data rappresenta una circonferenza di centro C(4, 3) e raggio R=5
Il punto A ha coordinate (8,0)
Il punto B ha coordinate (0,6)
Scrivo l'equazione della retta passante per A, B e verifico che C appartiene ad r
La retta (AB) ha equazione:
r: y = - (3/4)*x + 6
Verifico se C € r ==> 3 = - (3/4)*4 + 6 => 3=3 ok
76753
punti
Genius II
Ciao. L’equazione della circonferenza assegnata indica, per via della mancanza del termine noto c, che essa passa per l’origine. Il triangolo 0AB essendo rettangolo in O(0,0)ha ipotenusa AB il cui punto medio deve coincidere con il centro C della circonferenza.
94697
punti
Genius II
Le intersezioni fra gli assi (x*y = 0) e la data circonferenza
* Γ ≡ x^2 + y^2 - 8*x - 6*y = 0 ≡
≡ x^2 - 8*x + y^2 - 6*y = 0 ≡
≡ (x - 4)^2 - 4^2 + (y - 3)^2 - 3^2 = 0 ≡
≡ (x - 4)^2 + (y - 3)^2 = 25 = 5^2
di raggio r = 5 e centro C(4, 3) sono le soluzioni del loro sistema
* (x*y = 0) & ((x - 4)^2 + (y - 3)^2 = 25) ≡
≡ O(0, 0) oppure A(8, 0) oppure B(0, 6)
---------------
La verifica richiesta consiste nel vedere se AB è un diametro cioè nel calcolare
* |AB| = √(8^2 + 6^2) = 10 = 2*r
EBBENE SI': A, B, C sono allineati!
57383
punti
Genius I
