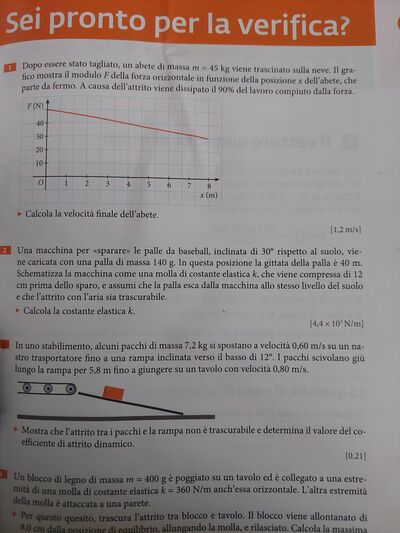
Dopo essere stato tagliato, un abete di massa $m=45 kg$ viene trascinato sulla neve. Il grafico mostra il modulo $F$ della forza orizzontale in funzione della posizione $x$ dell'abete, che parte da fermo. A causa dell'attrito viene dissipato il $90 \%$ del lavoro compiuto dalla forza.
Calcola la velocità finale dell'abete.
$[1,2 m / s ]$
numero 1
438
punti
Livello 1
Il lavoro della forza F orizzontale risulta essere pari all'area sottesa dalla funzione F(x) nell'intervallo [0,8].
Tale area risulta essere quella di un trapezio avente B=50, b=30, h=8
Quindi:
L= (50 + 30) * 8/2 = 320 j
A causa dell'attrito il 90% del lavoro viene dissipato, per cui risulta
L_effettivo = 320* (1 - 9/10) = 32 j
Sappiamo che il lavoro è pari alla variazione di energia cinetica. Quindi :
L= 1/2* m * V_finale²
Da cui si ricava
V_finale = radice ((2* L_effettivo) / m)
Sostituendo i valori numerici otteniamo :
V_finale = radice (64/45) = 1,19 m/s
76753
punti
Genius II
@stefanopescetto come bisogna risolverlo?
Ti ho scritto il procedimento
