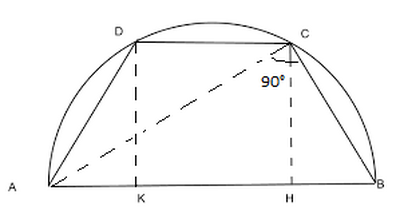
In un trapezio isoscele, inscritto in una semicirconferenza il cui raggio è lungo $20 \mathrm{~cm}$, la diagonale è $\frac{5}{4}$ della sua proiezione e la differenza delle loro misure è $6,4 \mathrm{~cm}$. Sapendo che il lato obliquo è $\frac{5}{3}$ della sua proiezione, calcola la lunghezza della base minore e il perimetro del trapezio.
139
punti
Livello 1
AC = 5AH/4
5-4 = 1 pu = 6,4 cm
AC = 6,4*5 = 32 cm
AH = 6,4*4 = 25,6 cm
CH = 6,4*3 = 19,2 cm (terna pitagorica 3, 4, 5)
AK = BH = (2*20-AH) = 14,4 cm
CD = AB-(AK+BH) = 40-28,8 = 11,2 cm
perimetro 2p = 40+11,2+2*24 = 99,2 cm
114207
punti
Genius II
