Considerazioni sugli enti fondamentali
- Consideriamo un punto A e disegniamo tutte le rette che passano per questo punto: ci rendiamo conto che sono infinite.
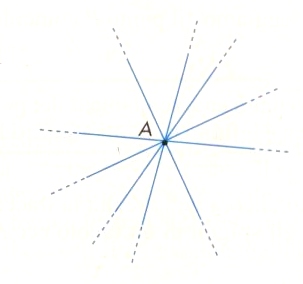 Diremo che:
Diremo che:
per un punto passano infinite rette che formano un fascio (o stella) di rette. - Consideriamo due punti A e B distinti e disegniamo le rette che passano per questi due punti: è intuitivamente vero che ne passa una e una sola.
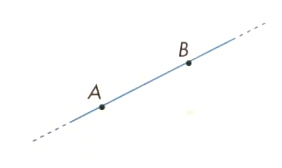 Diremo che:
Diremo che:
per due punti distinti passa una e una sola retta.
- Consideriamo tre punti qualsiasi A,B e C e disegniamo la retta che passa per questi tre punti. Ci accorgiamo subito che se i tre punti non sono allineati, non esiste alcuna retta che passi contemporaneamente per tutti e tre i punti.
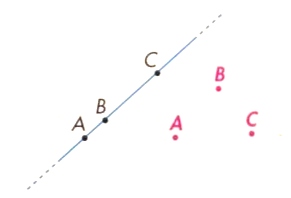 Diremo quindi che:
Diremo quindi che:
per tre o più punti passa una e una sola retta se sono allineati, nessuna in caso contrario. - Consideriamo tre punti A,B e C allineati e l’unica retta a che li unisce. Per quest’unica retta a, quanti piani passano? Ci rendiamo conto che ne passano infiniti.
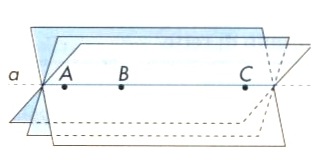
Diremo che:
per tre punti allineati, o per una retta, passano infiniti piani (o un fascio di piani). - Consideriamo tre punti A, B e C non allineati. quanti piani passano per questi tre punti? Passerà un solo piano.
 Diremo che:
Diremo che:
per tre punti non allineati passa uno e un solo piano.
